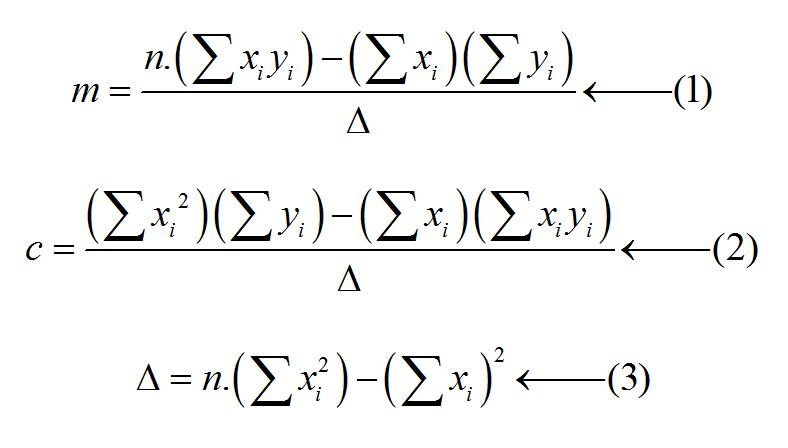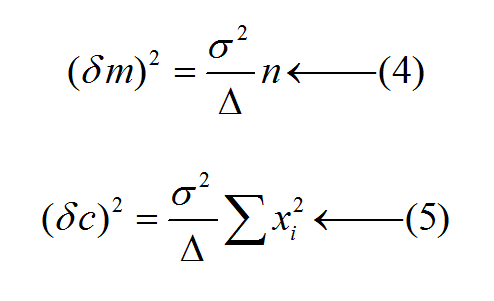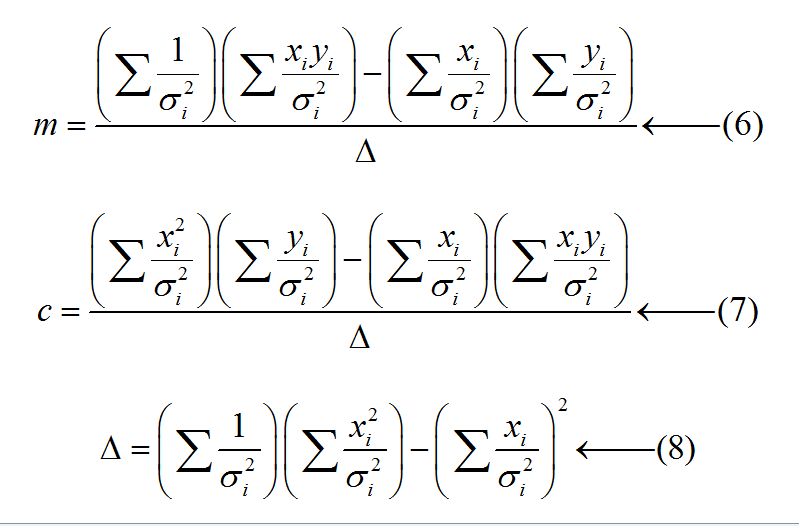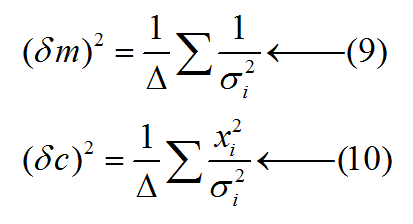Physics practical වලදි section 3 ලියද්දි ළමයින්ට තියෙන ලොකුම ප්‍රශ්නෙ තමයි, error calculations හරියට කරන එකයි, සුදුසුම විදිහට ප්‍රස්ථාර අඳින්නෙ කොහොමද කියන එකයි, ප්‍රස්ථාරයෙන් හරියට අනුක්‍රමණය හෝ අන්තඃඛණ්ඩය මැනගෙන අවසන් පිළිතුර දක්වා යන්නෙ කොහොමද කියන එකයි. හැබැයි මම මෙතනදි කතා කරන්න යන්නෙ හරියට error calculations කරන එකවත්, ප්‍රස්ථාර හරියට අඳින හැටිවත් නෙමෙයි. ඒ දෙකම අනිවාර්යෙන්ම වැදගත් උනත් අවසන් පිළිතුරට යන්න ප්‍රස්ථාරයේ අනුක්‍රමණය (m) හෝ අන්තඃඛණ්ඩය (c) නිවැරදිව හොයන විශේෂ ක්‍රමයක් තියෙනවා Least Squares Fitting කියලා. මේ ඒ ක්‍රමය භාවිතය ගැන පැහැදිලි කිරීමක්.

Physics practical වලදි බොහෝ වෙලාවට කරන්නෙ කිසියම් තත්ත්වයන් යටතේ යම් භෞතික රාශියක අගය සෙවීමයි. එහිදී ඊට අදාළ වන ගණිතමය සමීකරණයක් භාවිතයෙන් සහ කලින් design කරපු experiment එකක් භාවිතා කරලා මිනුම් උපකරණ එකක් හෝ කිහිපයක් භාවිතයෙන් පාඨාංක කිහිපයක් ලබා ගැනෙනවා. ඒසේ ලබා ගන්නා පාඨාංක ඍජුව හෝ තවත් සැකසීමකින් පසුව, කිසියම් විචල්‍යයක් මත තවත් විචල්‍යයක වෙනස්වීම වගුගත කරලා ඊට පස්සෙ ප්‍රස්ථාරයක් භාවිතයෙන් හෝ වෙනත් ක්‍රමයකින් ඒ අදාළ රාශියේ අගය සෙවීම සිදු කෙරෙනවා. මෙතනදි බොහෝ වෙලාවට එක් අගයන් යුගලයක් පමණක් භාවිතයෙන් පිළිතුරක් සෙවීමේදී වෙන්න පුලුවන් වැරැද්දෙ ප්‍රමාණය වැඩි නිසා, පාඨාංක හෝ දත්ත කිහිපයක් ඇසුරෙන් ගණනය කිරීම වඩා නිවැරදි නිසයි වගුගත කිරීමක් අවශ්‍ය වෙන්නෙ. වඩාත් සාධාරණ අගයක් ලබාගැනීමට මේ ලබාගත් පාඨාංක හෝ දත්ත යුගලයන් එවායේ ස්වායත්ත විචල්‍යය (Independent variable) එදිරිව පරායත්ත විචල්‍යය (Dependent variable) ප්‍රස්ථාර ගත කෙරනවා. ඒවායේ නියම විචලනය හඳුනා ගැනීමටත් මෙම ප්‍රස්ථාර ගත කිරීම වැදගත් වෙනවා.

තවදුරටත් සාධාරණ අගයක් ලබාගැනීමට වැදගත් වන්නේ ලකුණු කළ ලක්ෂ්‍යන්ට සාධාරණම රේඛාව ඇඳීමයි. සරලම උදාහරණය ලෙස විචල්‍යයන් අතර සමානුපාතික විචලනයක් පවතින අවස්ථාවක් සලකමු. වෙනත් වචන වලින් නම් y = mx + c ආකාරයේ ප්‍රස්ථාරයක් ලැබෙන අවස්ථාවක් සලකන්න. ලකුණු කළ සියලුම ලක්ෂ්‍යන් සහ ලක්ෂ්‍යන්ට (x සහ y ඛණ්ඩාංක යුගලයන්ට) අදාළව ඇති error bars සැලකිල්ලට ගනිමින් අඳින සාධාරණ සරල රේඛාවේ ජ්‍යාමිතිය මත, එහි අනුක්‍රමණය (m) සහ අන්තඃඛණ්ඩය (c) යන අගයන් රඳාපවතින බැවින් එම නිර්මාණය තරමක් සැලකිල්ලෙන් කළ යුතු වෙනවා. මෙහිදී භාවිතා කරන ප්‍රධාන ක්‍රම 2 කි. එනම්,

1. Graphical Method (ප්‍රස්ථාරික ක්‍රමය)

2. Analytical Method (විශ්ලේශනාත්මක ක්‍රමය) යන ක්‍රම දෙකයි.

Graphical method යනු gravity point එක හරහා අඳින ප්‍රධාන සරල රේඛාවට අමතරව තවත් සරල රේඛා දෙකක් උපයෝගී කර ගනිමින් අනුක්‍රමණය හෝ අන්තඃඛණ්ඩය සෙවීමයි. Analytical method යනු Least Squares Fitting නැතහොත් Linear Regression යන Statistical method එක ආධාරයෙන් අනුක්‍රමණය හෝ අන්තඃඛණ්ඩය සෙවීමයි. මෙම ක්‍රම දෙකම භාවිතයේදී වෙනස් වන අයුරු පැහැදිලිව දැනගැනීම ඉතා වැදගත්.

ප්‍රස්ථාර නිර්මාණයේදී එක් එක් ලක්ෂ්‍යයන්හි ස්වායත්ත විචල්‍යය සහ පරායත්ත විචල්‍යය යන අගයන් දෙකටම අදාළව uncertainty values (අවිනිශ්චිතතා අගයන්) පැවතියත් බොහෝ විට වැඩි සැලකිල්ලක් දක්වනුයේ ඒවායේ පරායත්ත විචල්‍යයේ uncertainty value එකට බැවින් එය අනිවාර්යෙන්ම ප්‍රස්ථාරයේ error bars ලෙස ලකුණු කළ යුතු වෙනවා. තවද, ලක්ෂ්‍යන්හී පරායත්ත විචල්‍යයේ uncertainty values සැලකීමේදී ප්‍රස්ථාර ආකාර දෙකකට වෙන් කළ හැකියි. එනම්,

1. සියලුම ලක්ෂ්‍යන්හී පරායත්ත විචල්‍යයේ uncertainty values එකිනෙකට සමාන වන අවස්ථාව

2. එක් එක් ලක්ෂ්‍යයන්හී පරායත්ත විචල්‍යයේ uncertainty values එකිනෙකට වෙනස් වන අවස්ථාව ලෙස.

පළමු ආකාරය සලකමු. සියළුම ලක්ෂ්‍ය වල uncertainty values සමාන වන අවස්ථාවේදී එක සමාන විශාලත්වයකින් යුතුව error bars දැකගත හැකිවිය නමුත් ප්‍රස්ථාරයේ පරිමාණය (scale එක) සමහ සැසඳීමේදී ඉහත ආකාරය තවත් ආකාර දෙකකට වෙන් කළ හැකියි.

i. Uncertainty value > ප්‍රස්ථාරයේ පරිමාණය(scale)

ii. Uncertainty value << ප්‍රස්ථාරයේ පරිමාණය

i හි සඳහන් පරිදි ප්‍රස්ථාරයේ පරිමාණයට වඩා uncertainty value එක සැලකිය හැකි පමණ විශාල වන විට පැහැදිලිවම error bars දැකගත හැකි වෙයි. මෙවන් අවස්ථාවකදී පහසුවෙන්ම ලක්ෂ්‍යන්ගේ සහ error bars වල විහිදීම සලකා Graphical method එක මගින් පිළිතුර සෙවීමට යා හැකියි.

නමුත් ii හි සඳහන් පරිදි uncertainty value එක පරිමාණය සමග සැසඳීමේදී නොසැලකිය හැකි තරම් කුඩා නම් error bars ලක්ෂ්‍යන්ටම ඌනනය වෙයි. එවන් අවස්ථාවකදී ලක්ෂ්‍යන්හී පිහිටීම පමණක් සලකා සාධාරණ සරල රේඛාව නිර්මාණයෙන් අගයන් සෙවීම වඩා නිරවද්‍ය නොවිය හැකි බැවින්, එහිදී least Squares Fitting method එක අනුගමනය කිරීම වඩා සාධාරණ වෙයි.

දැන් දෙවන ආකාරය සලකමු. එනම් ලක්ෂ්‍යයෙන් ලක්ෂ්‍යයට error bars වල ප්‍රමාණය වෙනස් වන අවස්ථාව. උදාහරණයක් ලෙස කාලය (T) පාඨාංකය  ලෙසත් T² පරායත්ත විචල්‍යය ලෙසත් පැමිණෙන විටක T² හී uncertainty value එක 2(T)(δT) ලෙස වෙනස් වෙයි. එවන් අවස්ථාවක මුල් පාඨාංකයේ සෑම ලක්ෂ්‍යකම δT නියතව පැවතියත් 2(T)(δT) හී අගය T ගේ වෙනස් වීම මත ලක්ෂ්‍යයෙන් ලක්ෂ්‍යයට වෙනස් වෙයි. එබැවින් error bars වල ප්‍රමාණය එක ලක්ෂ්‍යයෙන් ලක්ෂ්‍යයට වෙනස් වෙයි. මෙවන් අවස්ථාවක Graphical method එක යෙදීමට අවශ්‍ය වන gravity point හරහා අමතර සරල රේඛා නිරමාණයේදී යම් ගැටලුවක් මතු වෙයි. එනම් gravity point එකෙන් දෙපසටම සාධාරණ වන පරිදි ලක්ෂ්‍යයන්ගේ error bars සැලකීමේදී එම සරල රේඛා නිර්මාණය කළ නොහැකිවීමයි. එබැවින් මෙවන් අවස්ථාවකදී පරිමාණය සලකා error bars නිර්මාණය කල හැකි වුවත් නොවූවත් Graphical method එක යෙදීම කළ නොහැකි වෙයි.

වැදගත්ම කාරණය වන්නේ error bars නිර්මාණය කළ හැකි නොහැකිවීම මත හෝ ඒවායේ ප්‍රමාණ සමාන අසමාන වීම මත හෝ Least Squares Fitting method එක යෙදීමට බාධාවක් නොවීමයි. එබැවින් විශේෂයෙන් සඳහන් නොවන්නේ නම් ඉහත සඳහන් කල සියලුම අවස්ථාවන්ට එය යෙදීම වඩාත් සාධාරණ වෙයි.

දැන් Least Squares Fitting method එක යොදන ආකාරය බලමු.මේ ක්‍රමයේ ඇත්තටම කෙරෙන්නේ සමීකරණ කීපයක් මගින් අනුක්‍රමණය (m) සහ අන්තඃඛණ්ඩය (c) යන අගයන් හි වඩාත් හොඳම අනුමාන කිරීමක් (estimate). කලින් සඳහන් කලේ පරායත්ත විචල්‍යයේ uncertainty values වලට වැඩි සැලකිල්ලක් දක්වනවා කියලා. ඒ ස්වායත්ත විචල්‍යයේ uncertainty value එක පරායත්ත විචල්‍යයේ uncertainty value එක සමග සැසඳීමේදී නොසලකා හැරිය හැකිතරම් කුඩාය යන උපකල්පනය මත. මෙම සමීකරණ නිර්මාණය කරලා තියෙන්නෙත් ඒ උපකල්පනය මතමයි.

එලෙසම සකසාගත් දත්ත යුගලයන් (x_i , y_i) ලෙසත් yi හී uncertainty value එක σ_i ලෙසත් සලකමු. නැවතත් කලින් සඳහන් කල ආකාරයටම, uncertainty values නැත්නම් error bars ලක්ෂ්‍යයෙන් ලක්ෂ්‍යයට සමානවීම සහ අසමාඅන වීම මත මෙම  සමීකරණ වර්ග දෙකකට වෙන් කර දක්වන්නම්. Error bars සමාන වන විට එක් සමීකරණ කුලකයකුත් අසමාන වනවිට වෙනත් සමීකරණ කුලකයකුත් ආදේශයට යොදා ගත හැකියි. නමුත් සත්‍ය වශයෙන්ම තිබෙනුයේ error bars අසමාන අවස්ථාවට තරමක් සංකීර්ණ සමීකරණ කුලකයක් සහ error bars සමාන අවස්ථාවට එවායේ ඌනනයක් පමණයි. නමුත් පහසුව පිණිස පරායත්ත විචල්‍යයේ uncertainty values එකිනෙකට සමාන වන අවස්ථාවට අදාළ සමීකරණ පළමුවත්, අසමාන වන අවස්ථාවට අදාළ සමීකරණ දෙවනුවත් ඉදිරිපත් කරන්නම්.

1. පරායත්ත විචල්‍යයේ uncertainty values එකිනෙකට සමාන වන අවස්ථාව

විශේෂත්වය වන්නේ මෙම අවස්ථාවේදී y_i හී uncertainty value එක වන σ, අනුක්‍රමණය සහ අන්තඃඛණ්ඩය සෙවීමට භාවිතා කරන සමීකරණ වලට ඇතුලත් නොවීමයි. මෙහි n යනු භාවිත කල ලක්ෂ්‍යන් ගණනයි.

අවසන් පිළිතුරට අනුක්‍රමණය හෝ අන්තඃඛණ්ඩය භාවිතයෙන් අගය සෙවීමට අමතරව ඒවායේ uncertainty values වන δm සහ δc ද වැදගත් වෙයි. ඒවා පහත සමීකරණ ආධාරයෙන් සෙවිය හැක. මෙහි σ යනු පරායත්ත විචල්‍යයට පවතින පොදු uncertainty value එකයි.

2. පරායත්ත විචල්‍යයේ uncertainty values එකිනෙකට වෙනස් වන අවස්ථාව

පරායත්ත විචල්‍යයේ uncertainty values ලක්ෂ්‍යයෙන් ලක්ෂ්‍යයට වෙනස් වන අවස්ථාවේදී අනුක්‍රමණය හෝ අන්තඃඛණ්ඩය සෙවීමට භාවිතා කරන සමීකරණ වලට σ_i ඇතුලත් වන අතරම එබැවින් එම සමීකරණ තරමක් සංකීරණ ස්වරූපයක් ගනියි. එම අවස්ථාවට අදාළ සමීකරණ පහත දැක්වේ.

මෙම අවස්ථාවේ δm සහ δc සෙවීමට පහත සමීකරණ යොදා ගැනේ.

දැන් කළ යුතුව ඇත්තේ අදාළ දත්ත ඉහත සමීකරයණයන්හී අදාළ කුලකයේ නිවැරදිව යෙදීමෙන් අනුක්‍රමණයේ (m) සහ අන්තඃඛණ්ඩයේ (c) හොඳම අනුමානයන් සහ δm සහ δc නිවැරදිව ලබා ගැනීමයි. වඩාත් පහසුම ක්‍රමය වන්නේ ඉහත ආදේශයන් scientific calculator එකක් භාවිතයෙන් සෙවීමයි. පසුව එම අගයන් උපයෝගයෙන් අවසන් පිළිතුර නිවැරදිව ලබා ගත හැකියි.

Least Square Fitting මෙම ක්‍රමයේ ඇති තවත් ප්‍රධානතම වැදගත්කමක් නම්, ලක්ෂ්‍යන්ගේ දත්ත පමණක් දී ඇති විටෙක ප්‍රස්ථාරයක් නිර්මාණයකින් තොරව ඉහත අගයන් ලබා ගත හැකිවීමයි. එසේ වන්නේ ලක්ෂ්‍ය වල දත්තයන් කෙලින්ම සමීකරණයන් වල ආදේශ කිරීමෙන් අගයන් ලබා ගත හැකිවීමයි.

K.P.Siriwardena-Phy.Demo@2013 | kpsiriwardena@sci.cmb.ac.lk | KPS.CID@Feb 2014.