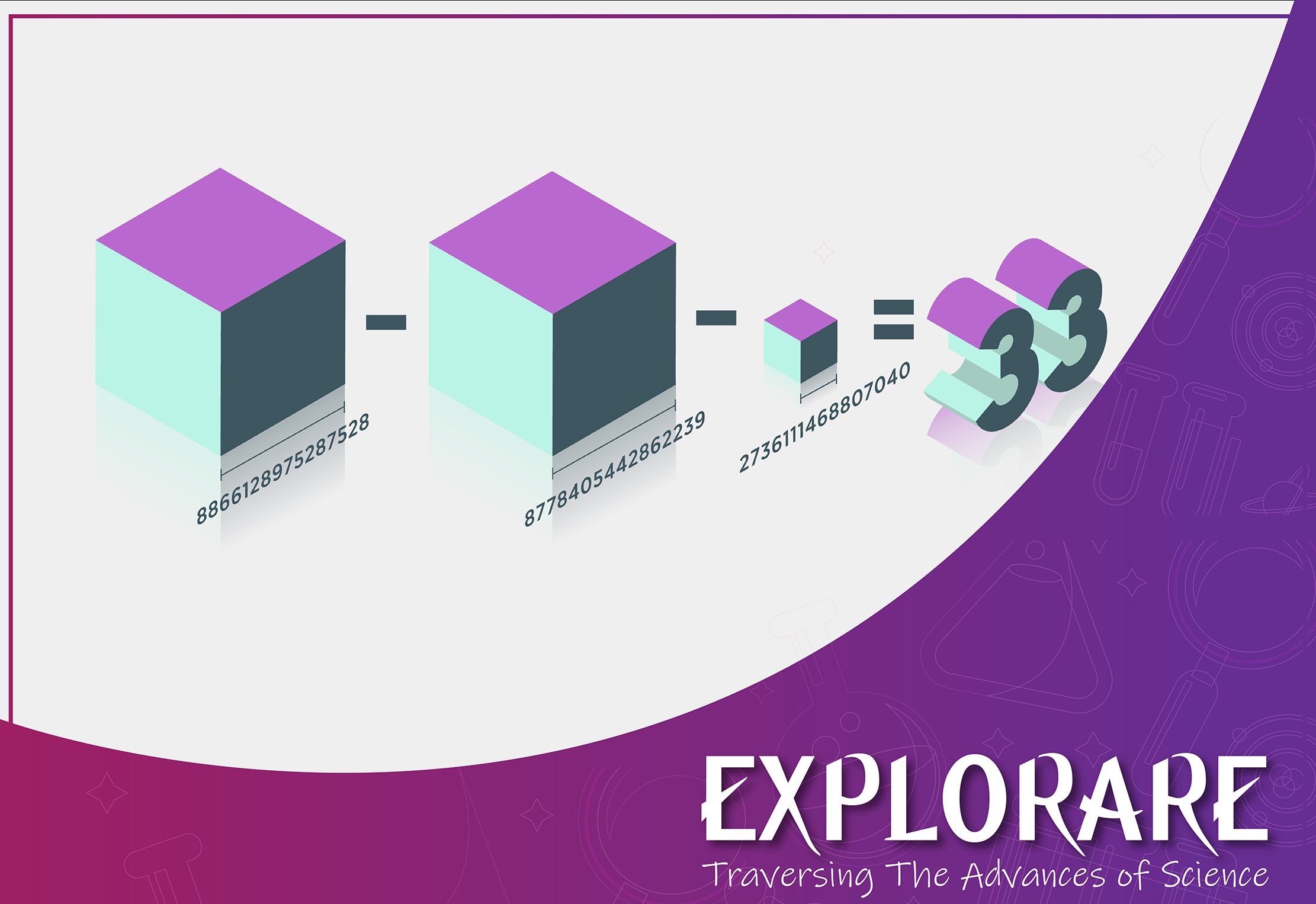
Let us write 29 as 29 = x³ + y³ + z³, plug in any integers for x, y, z. One set of solutions is 29 = 3³ + 1³ + 1³. Pretty simple and intuitive, right? Similarly, how about 30? Not so much. The only known solution involves numbers of 10 digits. Now, what about 33?
Well…. it took 65 years of trying with ever-improving computers to finally solve it in 2019, and the number of digits in all of x, y, z is a whopping 16! The problem was cracked by Andrew Booker from the University of Bristol using a program running on 512 CPU cores. He then went on to solve the equation for 42 a few months later with Andrew Sutherland from the Massachusetts Institute of Technology (MIT), aided by even more computing power. These discoveries fall under the work done on what is known as “the sum of three cubes” problem.
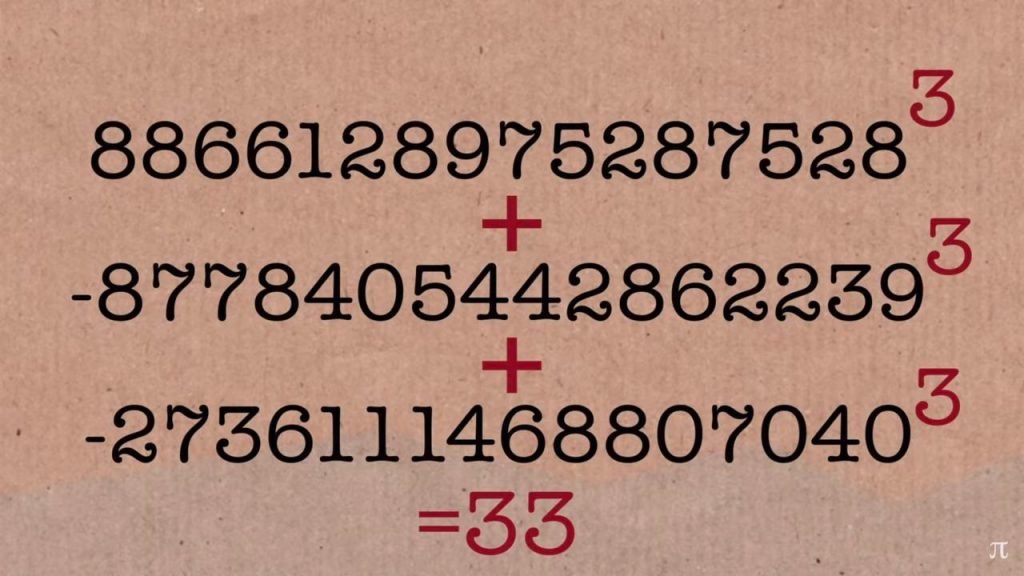
Sums of three cubes
The sum of three cubes problem involves identifying numbers that can be expressed as the sum of three cubes of integers (whole numbers with no fractional components.), that is, numbers that can be expressed as k = x³ + y³ + z³ where x, y, z are all integers.
These belong to the class of equations called “Diophantine equations”. By definition, they are equations involving only sums, products, and powers where all constants are integers, and the only solutions of interest are also integers. For example, 3x + 7y = 1, x² + y² = z² where x, y, z are all integers. Here, x = -2, y = 1 is a solution to the first equation and x = 3, y = 4, z = 5 is a solution to the second.
The focus here are the equations x³ + y³ + z³ = 33 and x³ + y³ + z³ = 42. This representation of 33 and 42 as a sum of three cubes has long evaded mathematicians, even with computational tools available since the 1950s. Apart from these two numbers, the rest of the integers from 1 to 100 could either be calculated as a sum of three cubes or could be proven to not have such a representation.
It is proven that if an integer ‘a’ is of the form a = 9k + 4 or a = 9k + 5 where k is any integer, or in other words, if the remainder when the integer is divided by 9 is 4 or 5, then it could not be written as the sum of three cubes. Hence some integers such as 4,5,13 and 14 cannot be written as such since 4 = 9 × 0 + 4, 5 = 9 × 0 + 5, 13 = 9 × 1 + 4 and 13 = 9 × 1 + 5.
As for the other integers, Roger Heath-Brown conjectured that there are infinitely many representations as a sum of three cubes for each of them (A conjecture is a mathematical statement that has not yet been proven perfectly, usually which has been formulated when one notices a pattern.) So far, at least one representation is known for many integers with some numbers such as 1 proven to have infinitely many representations.
Finding solutions for 33 and 42
You may have noticed that not being of the form a = 9k + 4 (or 5) is only a necessary condition for a number to be a sum of three cubes. In other words, if the number is a sum of three cubes, then it is not of those forms. We cannot use this statement the other way around and determine whether any number is a sum of three cubes. There is no known sufficient condition for it, that is to say, that there is no known condition such that ‘if *the condition is satisfied* then the number can be written as a sum of three cubes.
Hence the only possible way to know if numbers such as 33 and 42 can be written as a sum of three cubes and to know the solutions is to solve it by testing the vast number of possible solutions, with some clever bit of computer programming. The following is how Andrew Booker described simply, the process of solving the equation for 33 in an interview on the YouTube mathematics channel Numberphile. (Link in the references)
First x³ + y³ + z³ = 33 is rearranged as x³ + y³ = 33 – z³
Then by the expansion of x³ + y³,
(x + y)(x² – xy + y²) = 33 – z³
Now let x + y = d
Then,
(x² – xy + y²) = (33 – z³)/d
Now for all possible values of d and z (decided by the constraints imposed on the solving algorithms) the program checks if there are corresponding x and y values such that the equation is satisfied. Furthermore, since d, 33 – z³ and (x² – xy + y²) are also integers, it must be that d is a divisor of 33 – z³, and divisors of an integer are very few. Hence the few possible d values will be tested with z instead of all integers in the range set for d.
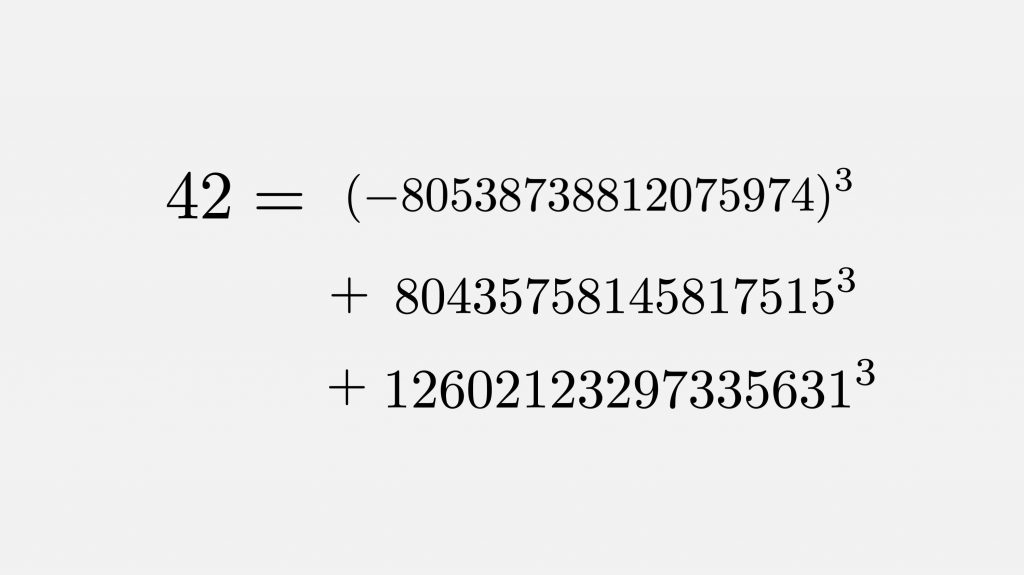
However, the solutions did not come easy, especially in the case of 42 which required 1.3 million computing hours on a global grid called the “Charity Engine” The programs returned the results shown in the 2 images above. As of April 2022, the only remaining unsolved cases up to 1,000 are 114, 390, 627, 633, 732, 921, and 975.
These discoveries generated lots of excitement in the mathematics community, due to the history of difficulty of this problem and the newfound knowledge. Also, the number 42 is of special interest in popular culture because in the whimsical science fiction novel The Hitchhiker’s Guide to the Galaxy by Douglas Adams, a supercomputer calculated “42” as the “Answer to the Ultimate Question of Life, the Universe, and Everything”.
The work done on 33 and 42 are appreciated for potential advancements in Number Theory and other fields of Mathematics that may be made using the results and mathematical methods employed here and also for the arguably more directly useful computer optimization methods which also were a major pillar in making these discoveries.
Written by: Pramudith Fernando
References:
- Booker, A.R. Cracking the problem with 33. Res. number theory 5, 26 (2019) https://doi.org/10.1007/s40993-019-0162-1
- https://www.britannica.com/science/Diophantine-equation#:~:text=Diophantine%20equation%2C%20equation%20involving%20only,y%2C%20and%20z%20are%20integers.
- The Uncracked Problem with 33 – Numberphile https://www.youtube.com/watch?v=wymmCdLdPvM&t=1s
- 42 is the new 33 – Numberphile https://www.youtube.com/watch?v=ASoz_NuIvP0
- The Mystery of 42 is Solved – Numberphile https://www.youtube.com/watch?v=zyG8Vlw5aAw
Image Credits:
- Cover image: https://bit.ly/3MwiEeM (Customized By Umesha Abeysuriya)
- Content image 1: https://bit.ly/3vQmA4q
- Content image 2: https://bit.ly/3yrfqW5