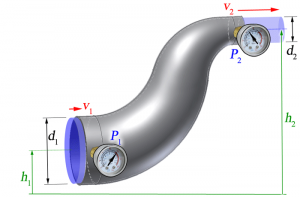
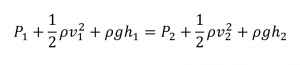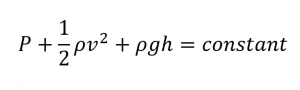Why would points of higher fluid speed have less pressure?

Have you ever wondered how a rabbit breathes inside an underground burrow? Ever wondered why a hurricane pulls everything up? What makes a 500 metric-ton Boeing 747 lift off the ground? All three of the above phenomena have one thing in common – they all have an airflow between two points of varying pressure. The study of airflow, belongs to the broad subject of fluid dynamics. It is the study of moving fluids. This article hopes to clarify one aspect of fluid dynamics which seems counter-intuitive at first glance.

The Theory

The physics behind the situations mentioned above, was formulated into a principle by Swiss mathematician and physicist, Daniel Bernoulli (1700-1782). He stated that:

“Where the velocity of a fluid is high, the pressure is low, and where the velocity is low, the pressure is high.”

Initially, this may seem counter-intuitive as one might expect the higher velocity of a fluid at a point, to exert a greater pressure. However, this is practically impossible as the higher pressure would slow the fluid down. Bernoulli was successful in developing this principle into an equation, enabling us to apply the principle quantitatively. For the derivation of Bernoulli’s equation, the flow must be assumed to be steady and laminar and the fluid incompressible, and the viscosity negligible. In such conditions, considering the flow of fluid between two points in a tube of non-uniform cross section that varies in height above an arbitrary reference level, the equation can be given as,

The above equation can be generalized for any point as,

Phenomena Associated with Bernoulli’s theorem

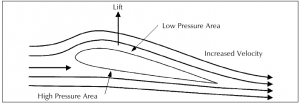Lift Produced by an Aircraft Wing

Aircraft wings and other airfoils are built such that most streamlines of air are crowded above the wing, rather than below it. Thus, the velocity of air moving above the wing is much higher than the velocity of air below the wing. This in turn results in the air pressure above the wing being lesser than the air pressure below the wing (according to Bernoulli’s principle), causing a net upward force termed as dynamic lift.

Hurricane

The sights of roofs flying off houses and windows being shattered, is a spectacular occurrence during a hurricane. The general impression given by most news reports about hurricanes is that the damage mentioned above is caused by the wind striking the houses, which is entirely wrong. The wind does contribute, but in an indirect manner. The speed of air above a house being hit by a hurricane is much higher than the air inside the house. This results in the pressure of air inside the house being much higher than the pressure of air just above it. Hence, according to Bernoulli’s principle, it is this pressure difference which causes the roofs to fly off.

Rabbit’s burrow

For a rabbit to survive in a burrow, there must be a circulation of air through it. The burrows are always made to have two openings. The slight differences in these two entrances ensure that the speed of air flow across them will be different. This difference of air speed results in a slight pressure difference between the two holes, forcing a flow of air through the burrow according to Bernoulli’s principle.

References:
1. Giancoli, D. C. (1985). Physics – Principles with Applications. New Jersy: Prentice Hall, inc.
2. Halliday, Resnick, & Walker, J. (2008). Fundamentals of Physics. New Delhi: Wiley India.
3. Hooper, H. O., & Gwynne, P. (1977). Physics and the Physical Perspective. New York: Harper & Row, Publishers, Inc.

Image Credits:
Fig 1: https://en.wikipedia.org/wiki/Daniel_Bernoulli#/media/File:ETH-BIB-Bernoulli,_Daniel_(1700-1782)-Portrait-Portr_10971.tif_(cropped).jpg
Fig 2: http://mechanicstips.blogspot.com/2016/02/bernoulli-equation.html
Fig 3: https://www.emaze.com/@AFQTFZWZ
Fig 4: https://www.embibe.com/learn/physics/concept-blowing-of-roofs-by-wind-storms-10715
Fig 5: https://content.iospress.com/articles/journal-of-facade-design-and-engineering/fde1645