Ruwimal • Science and Technology

In Search Of The Unchanging

June 3, 2022
by Ruwimal Pathiraja

Share

“Change is inevitable” as the old cliché goes. At least in the realm of reality, this is hard to argue with. On the other hand, in the mystical world of mathematics, we may stumble upon curious ideas that betray this tenet of nature. We call these ideas, “The Invariants”.

 

An invariant, put simply, is a property of a system that remains unchanged in spite of any transformations that the system may undergo. It is that which does not vary.

For a simple example, think of the process of counting. Say we have a finite number of people standing in a line and we wish to know how many people there are. We could start counting from the first person in the line and count (1…2…3…etc) backward towards the last person in the line. Or we could start with the last person and count forwards. Or, if we are in the mood for some self-inflicted pain, we could start from the middle and count forwards and backward alternately. There are obviously a lot of other ways as well. Irrespective of the method we choose to count, as long as we don’t count the same person twice or forget to count someone, we end up with the same total number of people. In other words, the number of people in the line is invariant of the process of counting.

 

In a game of chess, a bishop is restricted to only moving along diagonal paths on the chessboard. The coloring pattern of the chessboard then means that the bishop can never change colors on the board; a bishop starting on a dark square will always remain on a dark square and similarly for a white-squared bishop (because the diagonal paths on a chessboard consist of squares of the same color). Thus, no matter what state the rest of the pieces are in, we can always count on the bishops to be on the same color of square that they started on. This too is an invariant.

 

 

Now that we have a feel for what invariants look like, let’s look at how they are used to kill dragons (or not kill them).

A dragon has 10 heads. A knight can cut off exactly 1, 9, 7, or 3 heads, respectively, with one blow of his sword. In each of these cases, 10, 3, 19, or 0 new heads, respectively, grow on its shoulders. For example, if the knight cuts off 9 heads, exactly 3 new heads will grow back and if he cuts off 7 heads, exactly 19 new heads will grow back. If all its heads are cut off permanently, the dragon dies. Can the dragon ever die? How can you say for sure? Please think about this on your own before you read on. What is the invariant that helps the knight pick between chopping away and running away?

 

 

The key invariant is the remainder left when the number of heads is divided by 3 (also called remainder modulo 3). In each of the 4 possible cutting options, the number of heads of the dragon changes by 9, -6, 12, or -3 respectively. Each of these changes is divisible by 3!

This tells us that if the number of heads before a chopping event leaves a remainder of say 2 when divided by 3, then irrespective of the move the knight performs, the number of heads after the chopping will still leave a remainder of 2 upon division by 3 (because remainder upon division by 3 does not change after adding or subtracting a multiple of 3). Now the dragon starts off with 10 = 3×3 + 1 heads (a remainder of 1). We wish to get to 0 = 3×0 + 0 heads (a remainder of 0). But this is impossible since as we saw, the remainder of heads upon division by 3 is invariant of the chopping events. Sadly, the knight can never kill the dragon.

It will, I hope, please you to know that invariants have uses beyond the scope of medieval fantasy warfare. Broadly, the idea of invariants is used in diverse areas of mathematics such as geometry, topology, algebra, and discrete mathematics. Specifically, in computer vision, a sub-field of artificial intelligence, object attributes called “Hu moment invariants” (named after their discoverer M.K. Hu) were recently used to solve the Pathological Brain Detection (PBD) problem regarding brain diagnosis based on MRI scans. Additionally, the theory of optimizing compilers and formal methods for determining program correctness in computer science both employ the use of invariants.

Invariance is just one of the wide array of interesting techniques used by mathematicians to solve tough problems. Learning the rest (and discovering some of your own) only needs your appetite for a challenge to remain invariant 🙂 To help whet that appetite, I will leave you with a final puzzle based on invariants:

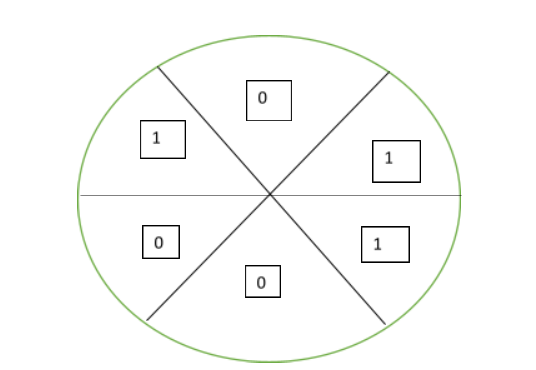
The figure below shows an oval divided into six sectors with a number written inside each sector. In each move, you are allowed to pick two adjacent sectors (sectors that share a common edge, where an edge is a line segment drawn from the center of the oval to its boundary) and increase each of the numbers in the two sectors by one. Is it possible to eventually reach a state where all the sectors have the same number written inside?

Happy hunting!

Image Courtesies

 

 
Tagged : / /