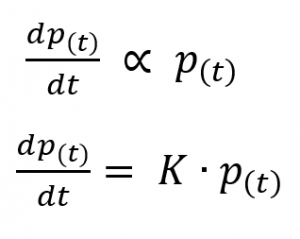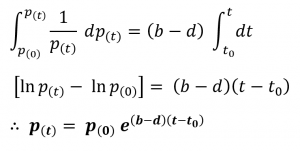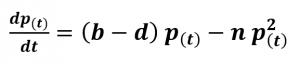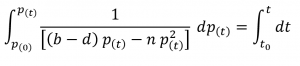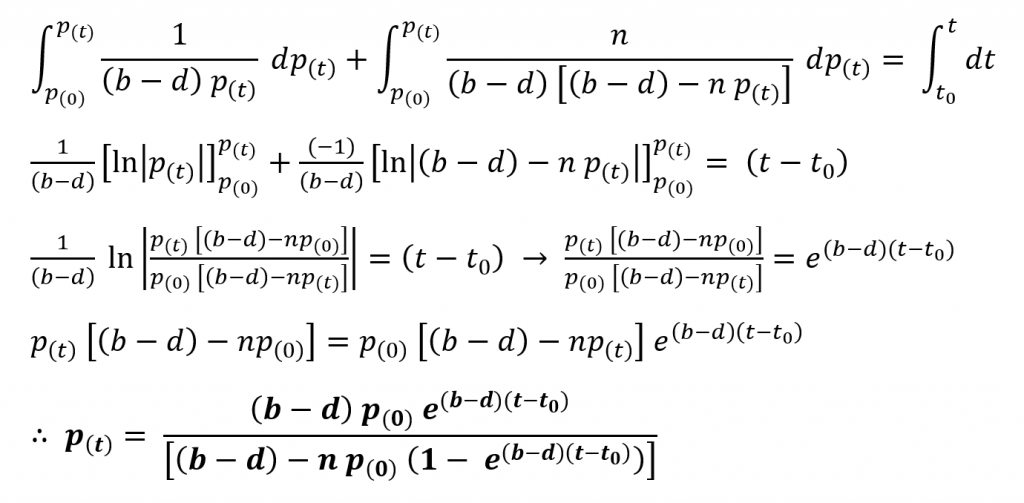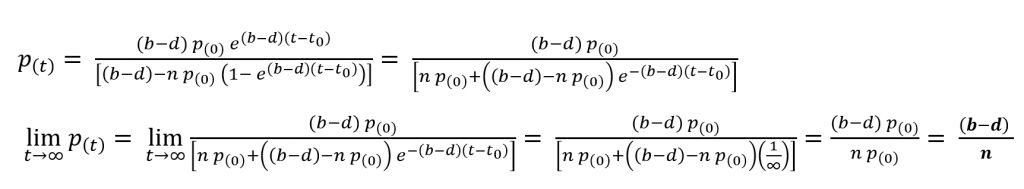Dasith • Science and Technology • Science Weekly

Mathematica de Naturae – I : Exponentially Problematic

March 28, 2020
by Dasith Tilakaratna

Share

With the turn of the new millennium; statisticians, ecologists, and mathematicians had to go head to head as the world faced a crisis with seemingly no possible solution. Summing up this crisis in one word: sustainability. According to the definition given by the United Nations, “sustainability” is meeting the needs of the present without compromising the ability of future generations to meet their own needs. The main requirement for coining this term is the massive population of the earth and the inadequacy of the earth to provide for and nurture a “destructive” species such as humans. Let’s take a look at how we can model population dynamics through mathematical ecology or ecological mathematics as it more appropriately seems to be.

The most basic factors to be considered when talking about population dynamics would be the birth and death rates of a certain species, say b and d respectively. Since we are dealing with dynamic or changing quantities, it is logical to assume a relationship in the form of a differential equation. Throughout this inquiry, we will be outlining certain constraints to our model.

Through calculus, we know that for a function to be differentiable it must be continuous as well. However, a species is not continuous when considering individual elements. However, if we add the constraint that the population of the species is considerably large we can regard unit changes in the population to be very small changes to the overall population, thus approximating it to be a continuous function.

Let’s assume that the rate of change of population (dp(t)/dt)  is proportional to the size of the population at that time p(t) itself.

Here K is the constant of proportionality. It can be assumed that the rate of change of population depends on the difference between the birth rate and the death rate of the species. Thus we can write down the above as follows;

This is a homogeneous linear first-order differential equation that was first formulated by the British mathematician and economist Thomas Malthus. Later it became the Malthusian Law of population. Let’s take a look at the solution to the above.

Assuming that the population of the species at a time t0 to be p(0)

Malthus argued that a population tends to increase exponentially based on a common ratio given by (b – d) while food supplies tend to grow at a constant and slower rate, which will inevitably lead to a shortage in food.

However, the Malthusian Law contained a simple flaw: the competition between the members of a species for resources. While to a certain limit, this law held for species with a comparatively short gestation period and lesser numbers confined in a given space, it fails to predict the growth of other species. Especially in our concern, it fails to predict the statistical data of human population dynamics.

By the year 1845, Belgian demographist Pierre Verhulst developed another model by taking into account a competition factor dependent on the size of the population at the given time as follows;

This is known as the Verhulst Law or more commonly referred to as the Logistic Law of population growth. The value of the constant n is very small in comparison to the term (b – d) which ensures that for small populations the competitive factor is very small and almost negligible while for very large populations there is a significant effect of the competitive factor to the rate of change of population. Let’s consider the solution to this first-order homogeneous non-linear differential equation.

We can see that the partial fractions for 1/(ax – nx2) are (1/ax)+(n/a(a-nx)) and using this,

This equation has a very interesting graphical representation. By investigating the limits of the solution to positive infinity we can see that the function converges to a value as follows.

Thus the prediction that a certain limiting or saturation value for population exists can be made. By investigating the stationary points of the function we can plot the graph for logistic growth as shown.

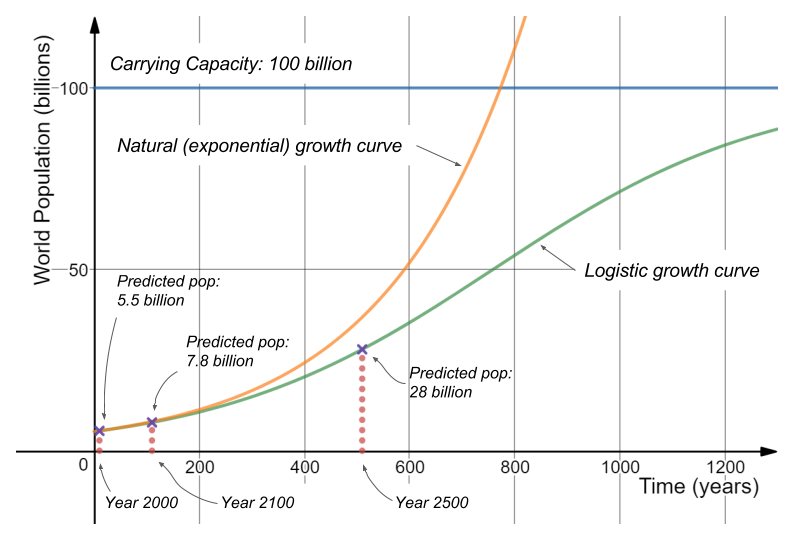
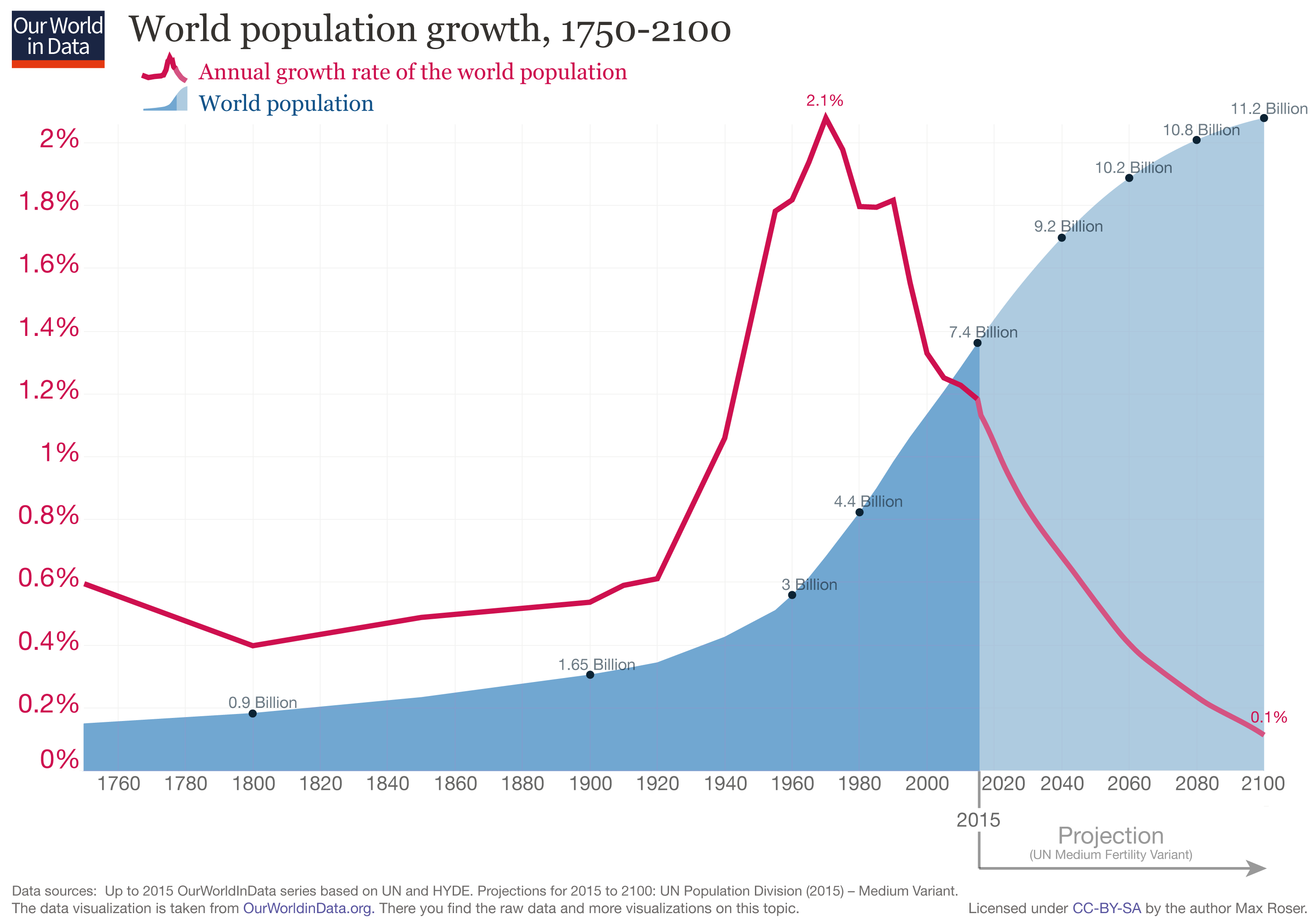
Figure 1: Comparison of Logistic Law and Malthusian Law

The Logistic law was implemented many years later after its discovery by Raymond Pearl in studying the population dynamics of fruit flies, bees and hens. Following its accurate and precise predictions, the equation is now applied to model human population growth as well, but its results are a terrifying shock to ecologists everywhere. The population growth rate is decreasing at an alarming rate as the carrying capacity is at the brink of exceeding.

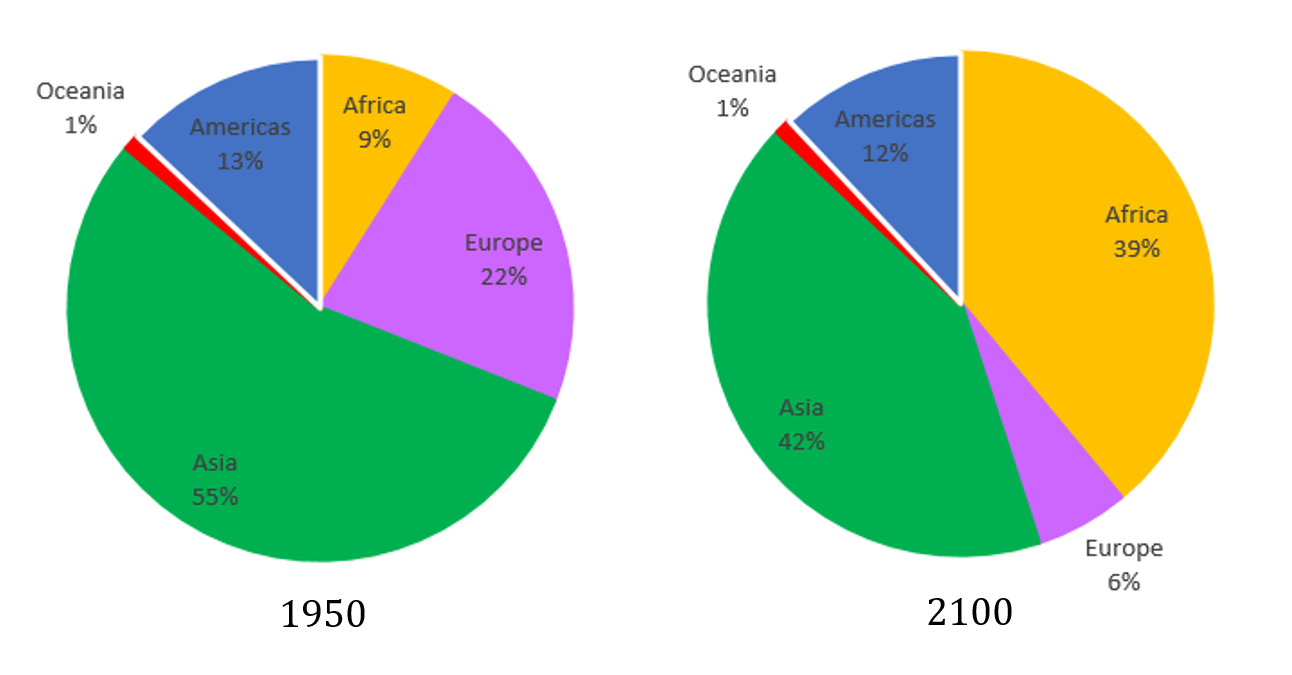
Figure 2: Comparison of the total population with the annual population growth rate

The following chart represents the variation of the population by continent from the year 1950 and the year 2100 as made with predictions based on the Logistic law of population growth.

Throughout history, the impact of overpopulation is quite devastatingly marked. As a species with a highly developed brain capable of harnessing technology to our only natural survival advantage, it is easy to notice that our only rivals in the food chain are ourselves. From an ecological perspective, this implies that we humans are at a very big level of competition to maintain our positions in the food chain from our competitors, in a civilized manner though. This basic competition progresses to the means through which we put food on our plates: an economic battleground is born. Enter politics and theology and we have paved our way to a global war even before 1914.

Apart from the more sociological aspects of human competition for survival, we must also consider the effect of disease, war, and medical advancements. The probability of the outbreak of a pandemic increases with the population due to the presence of more carriers. History has shown us many instances where death and disease have led to a mass wipeout of a population, though leading to a more stable and sustainable future: the Black Death, which claimed 75 million from a world of only 475 million led way to a complete cultural shift known as the Renaissance, the outbreak of the plague in England in the late 17th century led to what would be known as the breakthrough to change the world, the industrial revolution and the mass loss of lives from the Spanish flu and the world wars saw what was arguably the golden age of science and technology.

At the turn of the 22nd century, with an expected population of 11.2 billion, we must think from the 21st century onward on how to build up a sustainable environment if we are to bring a balance into the lives of those occupying this earth as well as to those who will be occupying it.

Reference :
Image Courtesy :
 
Tagged : / / / /