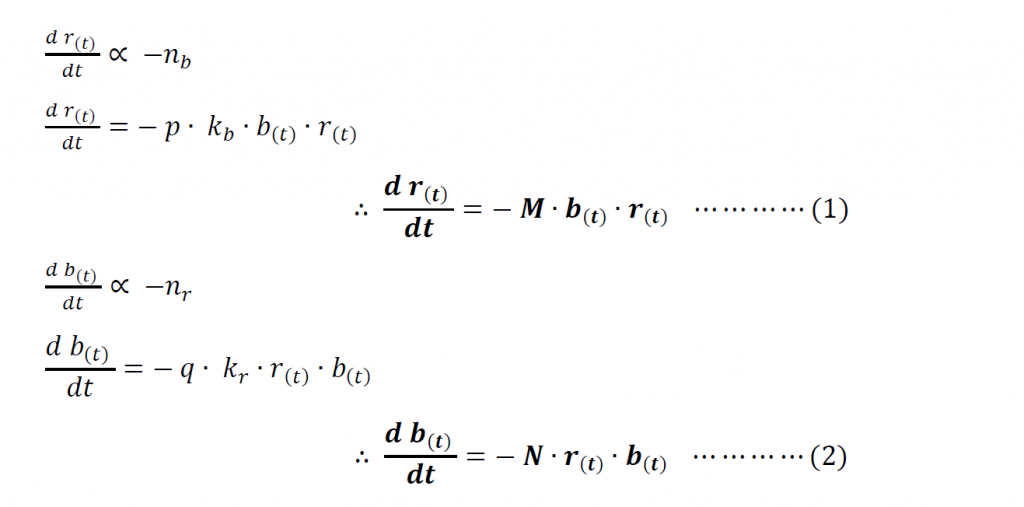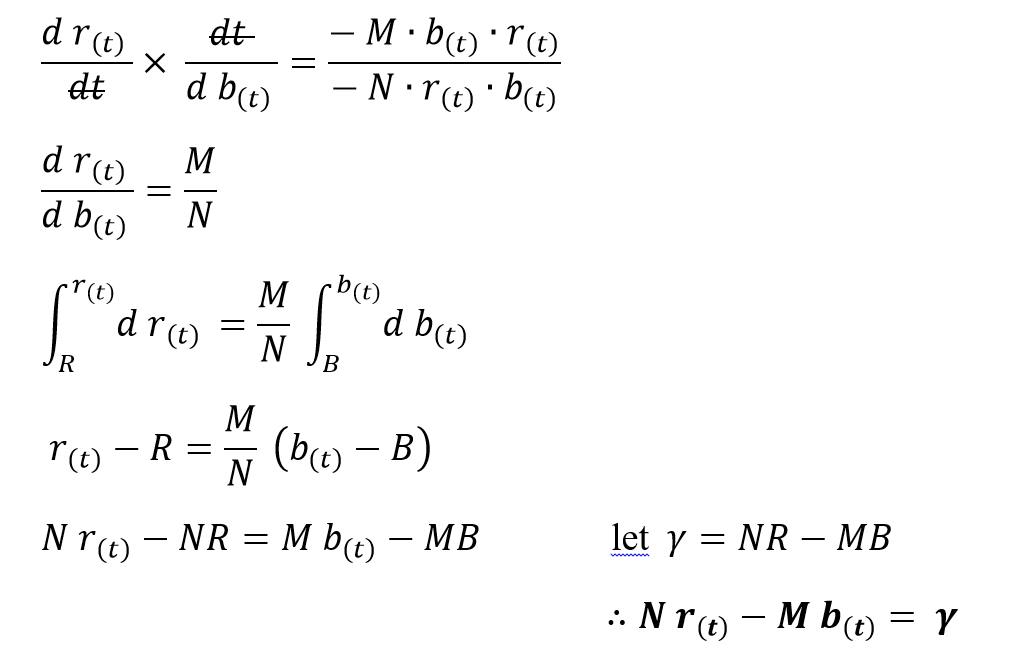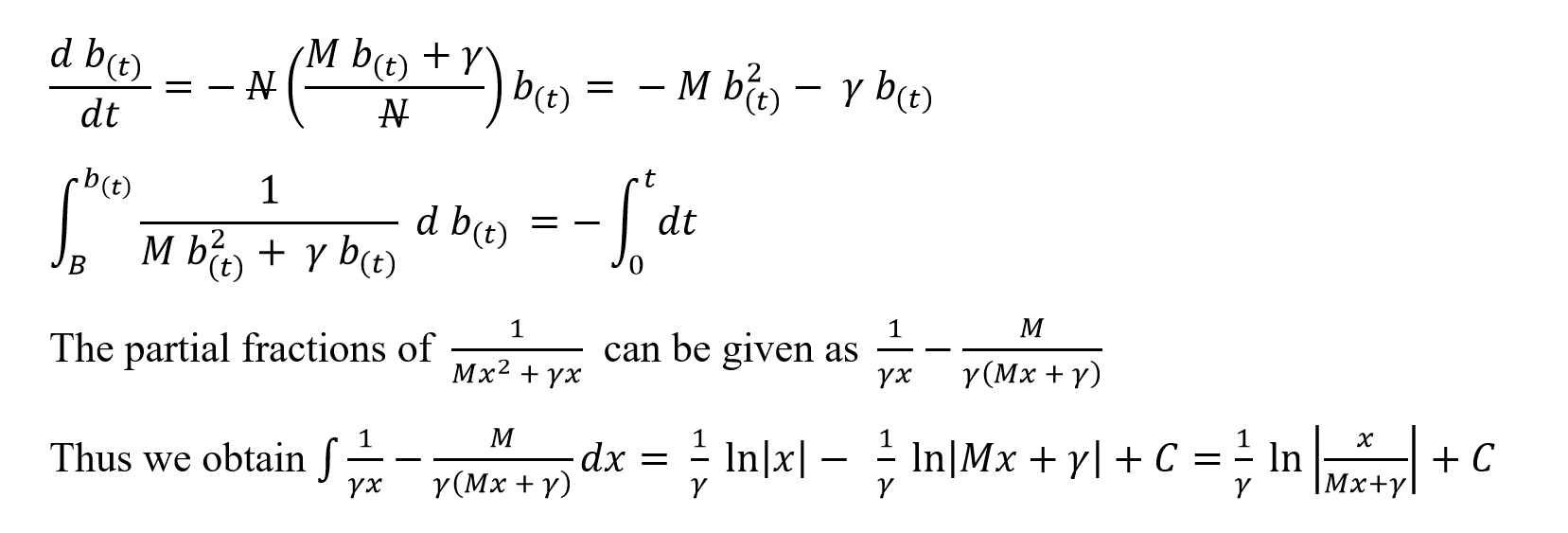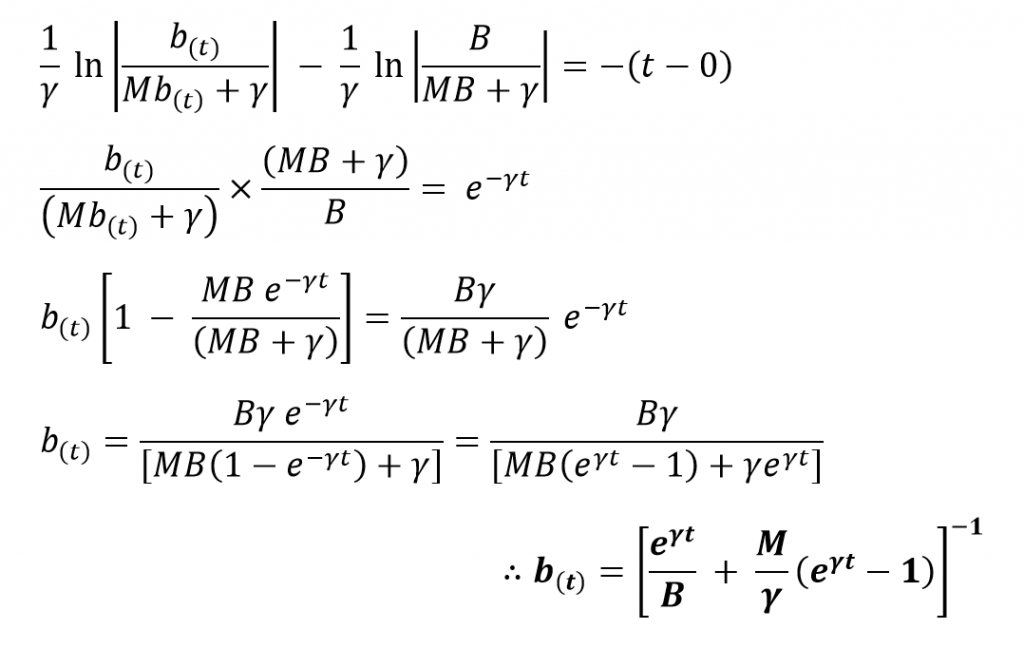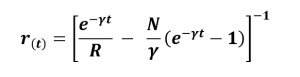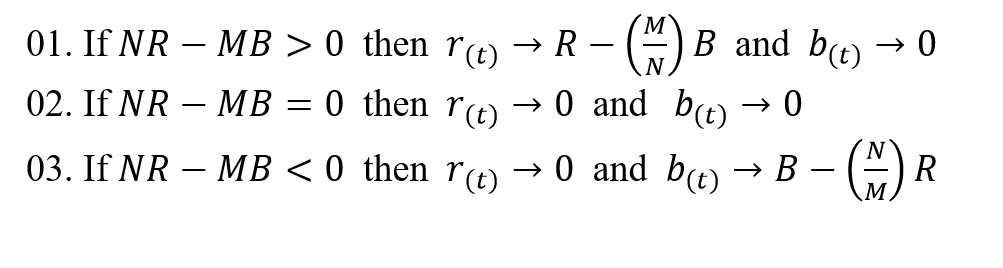As the dominant species of the planet, we are unrivaled in our position on the food chain. Evolution has led us down a very arduous path of invention and thought. Our natural ability to hunt has been erased from our genomes millennia ago. Thus, we are our own rivals in the food chain. However, our needs are more sophisticated. We have designed a set of rules for each individual in the form of law and legal discipline. We have also formed a code to which an individual must adhere through theology and philosophy. Finally, we have made means to solve disputes in these areas, by war and strategy. These strategies can be modeled in various ways according to the “type” of warfare involved.
In setting out these models we will consider two opposing forces as follows. A Red Army whose numbers at a given time is r(t) and a Blue Army of numbers b(t) at the same instance. The initial numbers of each army are R and B respectively. Let the combat effectiveness coefficient of the two armies be N and M respectively.
Ancient Warfare
Ancient warfare techniques can be stripped down to that of a cross between two swords. A formal, one-on-one combat zone where it is useless bringing more men to the battlefront. This reflects the inability of the sides to mass their forces effectively.
From this we can consider the number of attacking opportunities for the Red Army, nr is proportional to the number of combatants in the Red Army (r(t)), and the number of targets available in the opposing army (b(t)).
Similarly, we can write down the number of attacking opportunities for the Blue army, nb as follows.
We can assume here that no reinforcements are available at the battlefront for either army by considering the time taken for troops to travel. Thus, the rate of change in the numbers of one army is proportional to the number of firing opportunities of the opponent. Furthermore, it is a reduction in the numbers of the army as well. From this, we can obtain the following. Let the two constants of proportionality be p and q where they are both positive.
Before we analyze the above equations it is easier to start with the analysis of the numbers of one army with respect to the other.
Dividing (1) by (2)
These equations were first developed and forwarded by F.W. Lanchester, an engineer during the First World War. We refer to this as Lanchester’s Linear Law due to the linearity of the equation.
Lanchester’s Linear Law
In a battlefront, the winning side is that whose numbers are left unconquered at the end. The basic principle of ancient warfare is as such. Using the above equation we can now compare the numbers of each army with time easily.
Substituting for r(t) in equation (2)
Similarly, we can obtain an expression for r(t) by substituting b(t) into equation (1) as,
Let’s assume that at the end of the war, say after a time t = T, the Red army wins. That implies that bT = 0 and rT > 0.
Now let’s proceed to simulate a battle between the two armies by assuming that both sides have an equal initial strength of 16 men. Take the value of the combat effectiveness coefficient of the Blue army as 0.8 and that of the Red Army as a variable. Thus N must be greater than 0.8 for the Red Army to win. The y-axis denotes the strength of the army and the x-axis denotes the time that the war proceeds through.
Considering the above we can summarize the conditions for the outcome of a battle as follows.
Further Insights
The above conclusions are made assuming that the two armies deploy only one unit into the battlefield and that both army units use the same level of weaponry. But history rarely shows single unit battlefields. We can consider an adjustment as follows.
Let the number of Blue combatants be btot and the number of Red combatants be rtot. Consider the number of Blue combatants of type i to be bi (t) and the number of Red combatants of type j to be rj (t).
As ancient warfare would encompass terrestrial arenas we can classify units into a few categories as follows.
Infantry and Chariots
The first would be infantry, or in simple terms, foot soldiers. Throughout history, we have seen many nations and empires incorporating various forms of battle strategies. The Greeks were infamous for their Phalanx formation, depicted below.

The basic unit of the Phalanx was the speira, which consisted of around 256 spear-wielding men. Phalangites, who hefted 20 feet long pikes made up the outer ranks. Swordsmen were at a loss of breaching the ranks of the Phalanx while no horse could approach it without death. This strategic formation was the pivotal point for the immense success of Alexander the Great in expanding the Macedonian empire.
While various formations made foot soldiers invincible, the use of horses was further optimized by chariots. A chariot regularly consisted of a three men crew as follows. The charioteer, whose skill was what the success of deploying a chariot mattered mostly on. A warrior, fully clad in body armor and wielding long-range weaponry such as arrows or spears. And a shield-bearer to protect the other two as well as to jump into action if needed. The most famous users of the chariot were the Egyptians and the Hittites.
Siege Engines and Artillery
The third category is siege engines. While the Romans were notorious for their seas of legion soldiers, their biggest strategic advantage was their numerous ingenious war machines. These include ballistae capable of discharging weighted arrows or javelins, to various movable shed like battering rams. The Romans used a modified version of the Greek catapult, the onager to propel rocks to break through ranks of opponents as well as to collapse their fortresses.
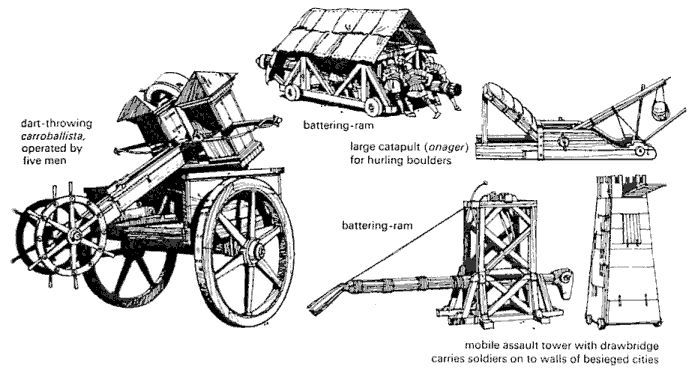
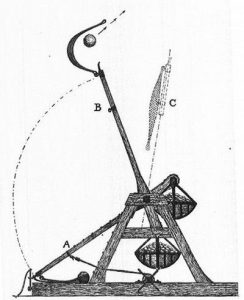
However, it was the Arabs that gave birth to the height of siege weapons in the medieval era. The counterweight trebuchet was the most feared weapon of mass destruction in the Crusades. Considered as the epitome of applied mathematics and mechanics in weaponry, various counterweights could propel specific masses to ranges of 200 m – 400 m. The counterweight trebuchet was mainly used to propel rocks, explosives, and infected bodies into enemy lines.
Meanwhile, the Asian peninsula saw the first models of artillery being used in battle. The Chinese used rockets that could be launched by soldiers or loaded on to launchers and fitted to carts. The existence of flamethrowers capable of shooting flames to distances of 10 m exemplifies the use of artillery devices. These ideas were further developed by Mongols and Koreans into devices that fired dozens of rockets or arrows in a single shot.
Lanchester’s Linear Law has very wide use in modern days in a much-unexpected area. Real-Time Strategy (RTS) games such as StarCraft, Rise of Nations, and Age of Empires utilize the estimated combat effectiveness coefficients of weaponry as mentioned above in creating complex and realistic simulations. To quote the great Chinese strategist Sun Tzu, “The ability to gain victory by changing and adapting according to the opponent is called genius”. And genius is something we encounter greatly in ancient warfare.
References:
01. Braun, M., 1993. Differential Equations and Their Applications. Fourth ed. New York: Springer Science+Business Media.
02. Karr, A.F., 1981. Lanchester Attrition Processes and Theater-Level Combat Models. 1st ed. Virginia: Institute of Defense Analyses.
03. Newark, T., 2016. The History of Warfare. 1st ed. New York: Chartwell Books.
Image Courtesies:
01.Featured image: https://bit.ly/39UwcN9
02.Image 1: https://bit.ly/2VcPfgt
03.Image 2: https://bit.ly/2USEUao
04.Image 3: https://bit.ly/2wmZM02