ඇත්තෙන්ම කොක්ක ඇණයක් වගේ දැනෙනවද ? කොක්ක අවුල් වගේ දැනෙනවද ? මේ දවස් වල අපේ විද්යා පීඨයේ පළමු වසරේ නංගිලා මල්ලිලාට වගේම අපේ දෙවෙනි වසරේ සහෝදර සහෝදරියන්ටත් තියෙන ලොකුම ප්රශ්නයක් තමයි මේ කොක්ක හෙවත් අනුකලනය. මෙය ඉතාමත් ගැඹුරු ගණිත කර්මයක් වුවත් මං ඒක ඉතාමත්ම සරලව කියල දෙන්නම්.එතකොට තේරේවි යකා කියන තරම් කළු නැහැ කියල.මං මේ ගමන ඔයාලට ගණිතයේ ඇති කලනය කොටස ඉතාමත් සරලව කියල දෙන්නයි හදන්නේ. මං ඔයාලව පුංචි කාලයට අරන් ගිහින් එතන ඉදන් ඉදිරියට එන්නම් 😀
ඔයාල පහේ පන්තියේ ඉන්නකොට ඉගෙන ගත්තනේ එකතු කිරීම, අඩු කිරීම ,ගුණ කිරීම සහ බෙදීම.ඒ තමයි ගණිතයේ තියෙන මුලික ගණිත කර්ම හතර. ඔයාල සාමාන්ය පෙළ දක්වා ගණිතයේ ඇති සියලුම සුත්තර ටික දාන්නේ මේ හතරෙන් තමයි.නමුත් උසස් පෙළ ගණිත විෂය හදාරන යට තවත් ගණිත කර්ම දෙකක් දැනගැනීමට ලැබෙනවා.ඒ තමයි අවකලනය සහ අනුකලනය. මේ දෙකම සමාන්තරව යන ගණිත කර්ම දෙකක්. මං මුලින්ම අවකලනය ගැන කියල දෙන්නයි හදන්නේ මේ ලිපියෙන්.
මොකක්ද මේ අවකලනය කියන්නේ ? සමහර අයට ලොකු අවුලක් වෙලා වගෙ ඇති මේ අවකලනය ගැන.මං ඉතාමත් සරලව කියල දෙන්නම් අවකලනය කියන්නේ මොකක්ද කියලා….
f(x) කියල සංකේතයක් ඔයාල දැකල ඇති.මේ කියන්නේ x වල ශ්රිතයක් කියන අදහස ගණිතමය ස්වරුපයෙන් දැක්වීමයි.මේ සංකේතයට බය වෙන්න එපා.අපිට ඕනේ නම් x වල ශ්රිතයක් (function of x) ලියන්න පුළුවන් g(x), h(x) යනාදී වශයෙනුත්….මේ සියල්ලෙන්ම අදහස් කරන්නේ මෙහි ඇත්තේ x වල ශ්රිතයක් බවයි.y වල ශ්රිතයක් අපිට ලියන්න පුළුවන් f(y), g(y) … යනාදී වශයෙනුත්. මං දැන් හිතනවා ඔයාල මේ සංකේතය පිළිබඳව දන ගත්තා කියල.ඉතින් දැන් අපි බලමු මෙම ශ්රිතය අවකලනය කරන්නේ කොහොමද කියල.
සංකේතාත්මකව අවකලනය සංකේතවත් කරන්නේ d/dx ලෙසටයි. උදාහරණයක් විදිහට මං f(x) කියල ශ්රිතයක් අවකලනය කරනවා කියල හිතමු.එක ලියන්නේ මෙන්න මෙහෙමයි
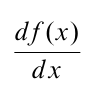
දැන් මට හිතෙනවා ඔයාල මේ සංකේතය ගැන යම්කිසි අවබෝධයක් ලබා ගත්තා කියලා.dx කියන්නේ x වල ඉතාමත් කුඩා අගයක්,ඒ වගේම dy කියන්නේ y වල ඉතාමත් කුඩා අගයක්.මේ සංකේතයෙන් කියන්නේ y කියන ශ්රිතය x විෂයයෙන් අවකලනය කරනවා යන්නයි (differentiating function f(x) with respect to x) .එහෙමත් නැත්තම් y වල ඉතාමත් කුඩා වෙනසකට සාපේක්ෂව සිදුවෙන x වල ඉතාමත් කුඩා වෙනස යන්නයි. අපිට x විෂයයෙන් පමණක්ම අවකලනය කරන්න ඕනේ නැහැ.උදාහරණයක් විදිහට ප්රවේගය කියන්නේ විස්තාපනය වෙනස් වීමේ සීග්රතාවය බව ඔයාල හොදටම දන්නවා. නමුත් වඩාත්ම නිවැරදි වන්නේ ව්ස්තාපනය කාලය විශයෙන් අවකලනය කල විට ප්රවේගය ලැබීමයි.ඒ වගේම ත්වරණය කියන්නේ ප්රවේගය වෙනස් වීමේ සීග්රතාවය බවත් ඔයාල හොදටම දන්නවා. නමුත් ගණිතමය ස්වරුපයෙන් කියූ විට ප්රවේගය කාලය විෂයයෙන් අවකලනය කල විට ත්වරණය ලැබේ ලෙසට විය යුතු වෙනවා.
විස්තාපනය s නම් ප්රවේගය v නම් කාලය t නම් සහ ත්වරණය a නම් මම කලින් කියපුවා කොහොමද ලියන්නේ කියල පෙන්නන්නම්.
v=ds/dt සහ a=dv/dt ලෙසට එව්වා ලිවිය යුතු වෙනවා.මම මේ වගේ ඉතාමත් සරල අවස්ථාවක් ගත්තේ ඔයාලට මට හැකි පමණ සරලව මෙම ගැඹුරු සංකල්පය කියා දීමටයි.
ඇත්තෙන්ම අවකලනය යන්නෙහි ජ්යාමිතික අර්ථකථනයකුත් තියෙනවා.යම්කිසි ශ්රිතයක් කීප වතාවක්ම අවකලනය කරන්න පුළුවන්. එකවතාවක් අවකලනය කලවිට පලවෙනි අවකලන සංගුණකය හෙවත් පලවෙනි ව්යුත්පන්නය ලෙසටත් දෙවෙනි වර අවකලනය කල විට දෙවෙනි අවකලන සංගුණකය හෙවත් දෙවෙනි ව්යුත්පන්නය ලෙසටත් කියනවා.ඒ වගේම තුන්වෙනි හතරවෙනි අවකලන සන්ගුනකත් තියෙනවා.මං පලවෙනි අවකලන සන්ගුනකයේ ජ්යාමිතික අර්ථ දැක්වීම ඉතාමත් සරල ලෙස ඔයාලට කියල දෙන්නම්…
ඔයාල දන්නවා ඇතිනේ xy ඛණ්ඩාංක පද්ධතිය.එහි ඇදී ඕනෑම ප්රස්තාරයක බෑවුම හෙවත් අනුක්රමණය තමයි පලවෙනි අවකලන සන්ගුනකයෙන් අර්ථ දක්වන්නේ.ඔයාල දන්නවා ප්රස්තාරයක අනුක්රමණය හොයන්නේ කොහොමද කියල.y ඛණ්ඩාංක අතර අන්තරය x ඛණ්ඩාංක අතර අන්තරයට දරන අනුපාතය තමයි එම ප්රස්ථාරයේ අනුක්රමණය හෙවත් බෑවුම කියන්නේ.ඒ කියන්නේ මෙන්න මෙහෙමයි.
අනුක්රමණය = y ඛණ්ඩාංක අන්තරය / x ඛණ්ඩාංක අන්තරය ලෙසටයි.ගණිතමය ස්වරුපයකින් කිව්වොත් මෙන්න මෙහෙමයි.අපි y=mx+c කියන ප්රසිද්ද සරල රේඛාව සලකමු.
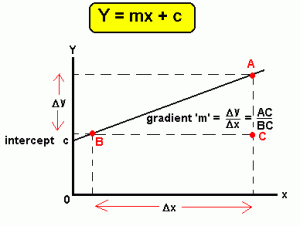
ඔන්න ඔහොමයි සරල රේඛාවක අනුක්රමණය හොයන්නේ.ඔයාලට පේනවා ඇති සරල රේඛාවක අනුක්රමණය නියත අගයක් කියල.ඒ වගේම සරල රේඛාව x අක්ෂයේ ධන දිශාව සමග සාදන කෝණයේ ටැන්ජන් අගය සේවිමෙන්ද එම සරල රේඛාවේ අනුක්රමණය හොයන්න පුළුවන් බව ඔයාලට පේනවා ඇති.අන්න එකත් සිහියේ තබාගෙන අපි දැන් වක්රයක අනුක්රමණය හොයන්නේ කොහොමද කියල බලමු.වක්රයක අනුක්රමණය ලක්ෂ්යයෙන් ලක්ෂයට වෙනස් වෙනවා.ඔයාලට ප්රශ්නයක් ඇති වෙනවා ඇති සරල රේඛාවක අනුක්රමණය නියත අගයක් වෙනවා නමුත් වක්රයක අනුක්රමණය වෙනස් වෙනවා කියල.අපි එව්වා වෙන්නේ කොහොමද කියල බලමු.ඇත්තෙන්ම වක්රයක අනුක්රමණය කියන්නේ වක්රයේ යම්කිසි ලක්ශ්යයකට අදින ස්පර්ශකය (tangent line) x අක්ෂයේ ධන දිශාව සමග සාදන කෝණයේ ටැන්ජන් (tan)අගයයි.
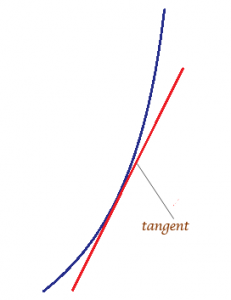
දැන් කලින් වගේ ඇඳපු ස්පර්ශකයේ අනුක්රමණය සෙවීමෙන් එම ලක්ෂ්යයේදී වක්රයේ අනුක්රමණය හොයන්න පුළුවන් ලේසියෙන්ම.ඒක හොයන වැඩේ මම ඔයාලට බාර දෙනවා.කිසිම අමාරුවක් නැහැ.කලින් මං කිව්වා සරල රේඛාවක අනුක්රමණය හොයන හැටි අන්න ඒ සිද්ධාන්තය පාවිච්චි කරලා ඔයාලට ලේසියෙන්ම අනුක්රමණය හොයන්න පුළුවන්.දැන් මං හදන්නේ ඔයාලට අවකලනයේ නීති රීති පැහැදිලි කරලා දෙන්නයි.
මුලින්ම කියන්න ඕනේ නියතයක් අවකලනය කලවිට පිළිතුර 0යි
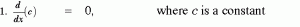
n කියල කියන්නේ ඕනෑම ධන හෝ ඍණ අගයයක් විට
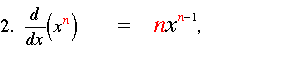
ඒවගේම ඝාතීය ශ්රිතය අවකලනය කල විට එම ශ්රිතයම ලැබේ.
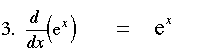
ප්රකෘති ලඝුගණකය(natural log) අවකලනය කල විට පහත පරිදි වේ.මෙහිදී x ධන විය යුතුවේ.
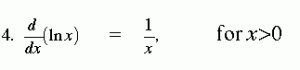
ඒ වගේම අනෙකුත් මුලික නීති පහත පරිදි වේ.
k යනු නියතයක් විට Kf(x) යන්න අවකලනය කල විට පහත පරිදි වේ.
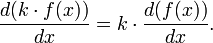
k=-1 විටදී
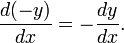
ශ්රිත දෙකක එකතුවක් හෝ අන්තරයක් ඇති විට, එම එකතුවේ හෝ අන්තරයේ අවකලනය වෙන වෙනම අවකලනය කර එකතුව හෝ අන්තරය ගත හැකිය.
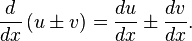
ඔයාල මෙහිදී මතක තබා ගත යුතු වන්නේ v සහ u යනු x වල ශ්රිත බවයි, එනම් u(x) සහ v(x) ලෙසට වේ.
ශ්රිත දෙකක ගුණිතය පහත පරිදි අවකලනය කල හැකිය….
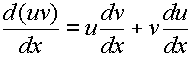
ඒවගේම ශ්රිත දෙකක අනුපාතයක් තිබ්බොත් ඒ කියන්නේ එම ශ්රිත දෙක බෙදීමකින් තිබ්බොත් (ලබ්ධියක් ලෙසට) අවකලනය කරන්නේ මෙන්න මේ විදිහටයි….
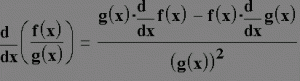
ඔයාල මේ ගුණිතයක අවකාලනයේදී සහ ලබ්ධ්යක අවකලනයේදී හොදට සිහියේ තබා ගත යුතු කාරණා කීපයක් තියෙනවා.ගුණිතයක අවකලනයේ පෙන්වා ඇති v සහ u යනු x වල ශ්රිත බව මෙන්ම ලබ්ධියක අවකලනයේදී පෙන්වා ඇති පිළිවෙලටම අවකලනය කල යුතු බව.නමුත් ගුණිතයක අවකලනයේදී එය බලපාන්නේ නැහැ.එම කාරණා ටිකත් ඔයාල හොදටම සිහියේ තබා ගන්න.මීලග වාරයේදී අපි බලමු ත්රිකෝණමිතික ශ්රිත අවකලනය කරන්නේ කොහොමද කියල ඒ වගේම කොහොමද දාම නිතිය පාවිච්චි කරලා ගණන් හදන්නේ කියල… ඕ ඕ අමතක උනා operators ගැනත් පොඩ්ඩක් මතක් කරන්න ඕනේ.ඒක නම් ගොඩක් වැදගත් වෙන්නේ අපේ දෙවෙනි වසරේ සහෝදර සහෝදරියන්ට තමයි.එහෙනම් ඊලග පාඩමෙන් නැවත හමුවෙමු… ඔයාලට ජය වේවා!!!

