ඔන්න ඉතින් අලුත් අවුරුද්දේ කොක්ක ගැන අලුත් පාඩමක් අරන් මං ඔයාල හම්බෙන්න ආවා.මේ කොක්ක ගැන ඒ කියන්නේ අනුකලනය ගැන පාඩම් මාලාවේ දෙවැන්නයි.ඔයාලට පාඩම් කිහිපයකින් මේ කොක්ක ගැන පැහැදිලි කරලා දුන්නට මේක එසේ මෙසේ කොටසක් නෙමෙයි.හරි…. මං ගිය වතාවේ ඔයාලට පොරොන්දුවක් දුන්නනේ ත්‍රිකෝණමිතික ශ්‍රිත (Trigonometeric functions) ගැනයි අවකලනයේ ඉතාම වැදගත් නීතියක් වෙන දාම නිතිය (chain rule) එකයි ඒවගේම operators ගැනයි කියල දෙනවා කියල.ඔන්න මං ඒ පොරොන්දුව ඉටු කරන්නයි යන්නේ.

මං හිතනවා ඔයාලට මං පසුගිය වාරයේදී කියලා දුන්න අවකලන නීති මතක ඇති කියල.දැන් අපි ඒවත් මතක් කරගෙන ඉස්සරහට යමු.ඔයාල ලෑස්තිද ??ඔන්න එහෙනම් අපි දැන් බලමු ත්‍රිකෝණමිතික ශ්‍රිත අවකලනය කරන්නේ කොහොමද කියලා.ඊට කලින් ත්‍රිකෝණමිතියේ ප්‍රධාන ත්‍රිකෝණමිතික අනුපාත මොනවද කියල බලමු.මං දන්නවා ඔයාල සාමාන්‍යපෙළ ගණිතයට මෙව්වා ඉගෙන ගෙන තියෙනවා කියල.කමක් නැහැ.අපි බලමුකෝ.

මං සෘජුකොණී ත්‍රිකෝණයක් සලකනවා.

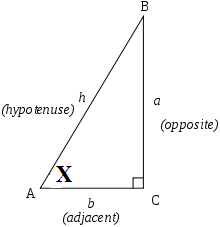
මේකේ opposite කියන්නේ සම්මුඛ පාදය adjacent කියන්නේ බද්ධ පාදය ඒ වගේම hypotenuse කියන්නේ කර්ණය.දැන් ඔයාල සෘජුකෝනි ත්‍රිකෝණයක පාද 3 හදුන්වන හැටි දැන ගත්තනේ.දැන් අපි ත්‍රිකෝණමිතික අනුපාත ලියමු.පොඩ්ඩක්වත් අමාරු නැහැ.හරිම සරලයි…

sin X = a/h
cos X = b/h
tan X = a/b

ඒ කියන්නේ sin X කියන්නේ සම්මුඛ පාදය කර්නයට දරන අනුපාතයයි.cos X කියන්නේ බද්ධ පාදය කර්නයට දරන අනුපාතයයි.ඒ වගේම tan X කියන්නේ සම්මුඛ පාදය බද්ධ පාදයට දරන අනුපාතයයි.සිංහලෙන් සයිනය කෝසයිනය සහ ටැන්ජනය කියල කියන්නෙත් මේ තුනටම තමයි.දැන් මං හිතනවා ප්‍රධාන ත්‍රිකෝණමිතික ශ්‍රිත පිළිබඳව අවබෝධයක් ඔයාල ලග ඇති කියල.ඔයාලට දැන් කරන්න පොඩි වැඩක් තියෙනවා.මට tan X කියන අනුපාතය sin X සහ cos X ඇසුරෙන් ලියල දෙන්න ඕනේ.හරිම සරලයි…ඔයාල උඩින් මං සඳහන් කල sin X සහ cos X අතර අනුපාතය අරන් බලන්න.එතකොට නිකන්ම tan X ලැබෙනවා.ඒ කියන්නේ sin X/cos X කියන්නේ tan X බවයි.එම සම්බන්ධය නම් ඔයාල අනිවාර්යෙන්ම සිහියේ තබා ගත යුතුය.

ප්‍රධාන ත්‍රිකෝණමිතික ශ්‍රිත වලට අමතරව තවත් අනුපාත 3ක් තියෙනවා.

sec X = 1/cos X
cosec X = 1/sin X
cot X = 1/tan X ලෙසටයි.තේරුනේ නැහැ වගේ නේද?ඉන්න… කලබල වෙන්නෙපා… 😀

අපි කලින් ලියපු ත්‍රිකෝණමිතික අනුපාත වල පරස්පරය තමයි මේ අලුතෙන් මං කියපු අනුපාත වල තියෙන්නේ.ඔයාල මන කලින් ලියපු අනුපාත වල පරස්පර අරන් පරික්ෂා කරලා බලන්න.කිසිම අමාරුවක් නැහැ.හරිම සරලයි.ඒ වගේම මම කලින් කිව්වා නේද sin සහ cos ඇසුරෙන් tan ලියන්න පුළුවන් කියල.ඒවගේම sec සහ cosec ඇසුරෙන් cot ලියන්නත් පුළුවන්.ඔයාලත් එක උත්සහ කරලා බලන එක ගොඩක් වටිනවා.එතකොට තමයි ඔයාලට මේ කොටස් මතක තියෙන්නේ……

දැන් අපි බලමු ත්‍රිකෝණමිතික ශ්‍රිත අවකලනය කරන්නේ කොහොමද කියලා.මුලික ත්‍රිකෝණමිතික ශ්‍රිත අවකලනය කරන හැටි මං පහතින් පෙන්වල දෙන්නම්…මං හැම වෙලාවේම කියනවා වගේ පොඩ්ඩක්වත් අමාරු නැහැ….

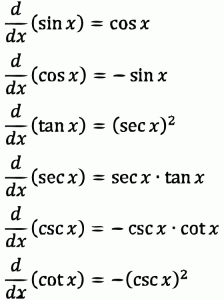
මේකේ තියෙනවා නේද csc x කියල එකක්? මම එහෙම එකක් කියල දුන්නේ නැහැ කියල දැන් කියාවි. බය වෙන්නෙපා එතනින් කියන්නෙත් cosec x කියන එකම තමයි.ලේසියට කෙටි කරලා තිබ්බට පොඩ්ඩක්වත් බය වෙන්න එපා. 😀

දැන් ඔයාල මේ සම්බන්ධයෙන් ඇති ගැටළු හොයන් කරන්න ඕනේ තනිවම.අවකලනයේ තව මුලික සිද්ධාන්තයක් කියලා දුන්නම අවකලනයේ ඔයාල දැනගන්න ඕනේ කොටස ඉවර වෙනවා… නමුත් අපි එක විචල්‍යක් විතරයි අවකලනය කලේ.විචල්‍ය 2ක් හෝ ඊට වඩා ආවම තමයි ආංශික අවකලනය කරන්නේ…ඔයාල ඩාබ ඩාබ කියන්නේ ඔන්න ඕකට තමයි….මම ඒ කොටසත් අනිවාර්යෙන්ම කියල දෙනවා..

දැන් අපි බලමු අවකලනයේ ශ්‍රිතයක ශ්‍රිතයක් අවකලනය කරන්නේ කොහොමද කියල…ඒ කියන්නේ දාම නිතිය පාවිච්චි කරන්නේ කොහොමද කියල බලමු…පොඩ්ඩක්වත් අමාරු නැහැ මෙව්වා…

අපි හිතමු අපිට අවකලනය කරන්න මෙන්න මේ වගේ එකක් දුන්නා කියල…

y = sin(2x+1) අපිට dy/dx හොයන්න කියලා දුන්න කියල හිතමු….

ටිකක් බය වුනා වගේ නේද? කොහොමද මේ වගේ දෙයක් කරන්නේ ? බය වෙන්නෙපා මම කියල දෙන්නම් මේක විසඳන හැටි …පරිස්සමින් බැලුවොත් ඔයාලට පේනවා sin ශ්‍රිතය ඇතුලේ x වල ශ්‍රිතයක් තියෙනවා කියලා.

අපි මුලින්ම මෙන්න මේ වගේ ක්‍රමයක් කරමු.
අපි u = 2x+1 කියල ගමු.
එතකොට අපිට දුන්න ශ්‍රිතය y = sin (u) බවට පත් වෙනවා.ඔයාලට ඒක පෙනුනා නේද ?
මතකද මම කලින් වාරයේ ශ්‍රිත ගැන කියල දුන්නා? කලින් y කියන්නේ x වල sin ශ්‍රිතයක් වුනාට දැන් y කියන්නේ u වල sin ශ්‍රිතයක්…

chain rule,එහෙමත් නැත්තම් දාම නිතිය අපිට මෙන්න මෙහෙම කියන්න පුළුවනි.

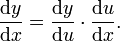
මේකෙන් කියන්නේ y කියන ශ්‍රිතය u විශයෙන් අවකලනය කරන්න ඕනේ..ඒ වගේම u කියන ශ්‍රිතය x විශයෙන් අවකලනය කරන්න ඕනේ.අන්න ඒ අවකලනය කරපු යුගලය ගුණ කල විට තමයි dy/dx වෙන්නේ.තේරුනේ නැහැ වගේ නේද ? අපි එක කලින් ගත්තු නිදසුනෙන් ම බලමු…

u = 2x+1 කියලනේ අපි ගත්තේ, එහෙනම් du/dx = 2 වෙනවා.

y = sin(u) නේද එහෙනම් dy/du කියන්නේ cos(u) වෙනවා.ඔයාලට මතක ඇතිනේ මම ත්‍රිකෝණමිතික ශ්‍රිත අවකලනය කරන හැටි කියල දුන්නා..ඉතින් දැන් තමයි එව්වා පාවිච්චි කරන්න ඕනේ අවස්ථාව…

එහෙනම් දැන් අපි dy/dx හොයමු.
කලින් මම කිව්වා දාම නීතියේ සමීකරණය පාවිච්චි කලොත් …

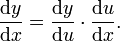
එතකොට dy/dx = cos(u) x 2 වෙනවා. අපි u කියන එක අතින් දාපු එකක් නිසා අපි u කියන එක වෙනුවට 2x+1 ආදේශ කල යුතු වෙනවා.
එතකොට අපිට ලැබෙනවා dy/dx = sin(2x+1) x 2
dy/dx = 2sin(2x+1) ලෙසට අවසාන පිළිතුර ලැබෙනවා.

ඔයාල දැන් y = ln(cos x) කියන ශ්‍රිතය අවකලනය කරන්න උත්සහ කරන්න ඕනේ.මම උදව්වක් දෙන්නම් u = cos x විදිහට ගන්න…
එතකොට y = ln(u) විදිහට ශ්‍රිතය වෙනස් වෙනවා….ඊලගට සාමන්‍ය විදිහට මම කලින් කියල දුන්නු පියවරවල් අනුගමනය කරන්න.හරිම සරලයි..
උත්තරේ වෙන්න ඕනේ dy/dx = -(sin x/ cos x)කියන එකයි. ඒ කියන්නේ පිළිතුර -tan x වෙනවා.දැක්කනේ … හරිම සරල පියවරවල් කිහිපයක් අනුගමනය කලාම ඉතාම පහසුවෙන් පිළිතුර ලබා ගන්න පුළුවනි.මෙම ක්‍රමය පුහුණු වීමෙන් හිතෙන් වුනත් මේ වගේ ගැටළු විසදන්න පුළුවන්.එය ලබා ගත හැක්කේ පුහුණු වීමෙන් පමණක් බවත් ඔයාල සිහියේ තබා ගන්න ඕනේ…

එහෙනම් මේ වාරයේ ඔයාල ගොඩක් දේවල් ඉගෙන ගත්තානේ…මට operators ගැන නම් කියන්න හම්බුනේ නැහැ මේ වතාවේ.. අපේ 2වෙනි වසරේ සහෝදර සහෝදරියෝ දුක් වෙන්න එපා..මම ඊලග වාරයේ operators ගැන වගේම ආංශික අවකලනයත් කියල දෙනවා අනිවාර්යෙන්ම..ආංශික අවකලනය කියල දෙනකොට පහුගිය අවකලන නීති මතකයේ තබා ගත යුතු වෙනවා.එකත් ඔයාල හොදට මතකයේ තබා ගන්න ඕනේ.මොකද මේ හැම දේකම එකිනෙක සම්බන්ධයක් තියෙනවා.එහෙනම් අපි ඉක්මනින්ම නැවත මුණ ගැහෙමු.ජය වේවා !!!!!