ඔයාල කලින් වාරයේ අවකලනයේ මුලිකම සිද්ධාන්ත කොටස් දැනගත්ත නේද ? දැන් අපි චුට්ට චුට්ට ඉස්සරහට යමු… මම හිතනවා දැන් ඔයාලගේ බය අඩුවෙලා කියල පොඩ්ඩක් හරි… එහෙනම් අපේ තුන්වෙනි පාඩමෙන් අපි ඉගෙන ගමු ආංශික අවකලනය ගැන.අපේ අණුක ජීව විද්‍යාව සහ ජීව විද්‍යාව කරන පළමු වසරේ නංගිලා මල්ලිලාට ආංශික අවකලනයේ ගැඹුරටම ඉගෙන ගන්න දෙයක් නැහැ.ඉතාමත් සරල සිද්ධාන්ත කිහිපයක් තමයි තියෙන්නේ. එහෙනම් අපි පටන් ගමු නේද ? ඕ ඕ මේකත් කියලම පටන් ගන්න ඕනේ… ඔයාල දැන් මුලික අවකලන නීති ඔලුවේ තියන් ඉන්න ඕනේ හොදද?

ඔයාල අවකලනය කලේ එක විචල්‍යක් ( variable ) තියෙනකොට විතරනේ, නමුත් ආංශික අවකලනයේදී අපි විචල්‍ය එකකට වඩා තියෙන ශ්‍රිත අවකලනය කරනවා. පොඩ්ඩක්වත් අමාරු නැහැ. එහෙනම් අපි බලමු කොහොමද ඒවා කරන්නේ කියල….

මං මුලින්ම බලන්නම් අපේ මුල්ම පාඩමේ ශ්‍රිත ගැන මම කියපුව ඔයාලට මතකද කියල.. ඔයාල ස්වයං පුනරීක්ෂණයක යෙදෙන්න ඕනේ. x කියන විචල්‍යය අඩංගු ශ්‍රිතයක් අපිට f (x ) විදිහට සාමාන්‍යයෙන් ලියන්න පුළුවන් කියල ඔයාලට මම කිව්වා මතක ඇති නේද ? ඒ වගේම z කියල තියෙන විචල්‍යයක් අඩංගු ශ්‍රිතයක් අපිට f (z ) විදිහට ලියන්නත් පුළුවන්. නැතිනම් අපිට g (z ) , g (x ) විදිහට ලියන්නත් පුළුවන් කියල මම කිව්වා ඔයාලට මතකද ?ඔයාලට ඒවා අමතක නම් මෙන්න මේ link එකෙන් ගිහිල්ල බලන්න පුළුවන් පහසුවෙන්ම. මම මේ තරම් ශ්‍රිත ගැන ඔයාලට කියන්නේ ඔයාලගේ සමහර කට්ටිය සමහර අංකන දැක්කම බය වෙනවා. මට ඕනේ කරන්නේ ඒ බය නැති කරලා ඔයාලට ඉතාමත් විනෝදයෙන් සහ සරලව මේ ගැඹුරු ගණිත කොටස් කියල දෙන්නයි 😀

දැන් ඔයාල දන්නවා f (x ) කියන සංකේතයේ තේරුම… එහෙනම් අපි ඉස්සරහට යමු නේද ? ඔයාල ලෑස්තිද ? ඔන්න යමු. අපිට x සහ y කියන විචල්‍යයන් දෙකක් පමණක් අඩංගු ශ්‍රිතයක් f (x ,y ) විදිහට ලියන්න පුළුවන්. එහෙනම් මට කියන්න ඕනේ ඔයාල x , y සහ z කියන විචල්‍යයන් 3 අඩංගු ශ්‍රිතයක් අංකනය කරන්නේ කොහොමද කියලා ????? හරිම සරලයි f (x ,y ,z ) විදිහට තමයි අපි අංකනය කරන්නේ…. දැන් මම හිතනවා ඔයාලට විචල්‍යයන් එකකට වඩා තියෙන ශ්‍රිත හදුනා ගන්න පුළුවන් කියල…

දැන් ඔයාල dy /dx කියන සංකේතයේ තේරුම දන්නවා… එක අමතක නම් මම කලින් සඳහන් කරපු link  එකට ගිහින් බලන්න පුළුවනි. එතකොට ඔයාලට අමතක ඒවා මතක් කරගන්න පුළුවන්. දැන් අපි යනවා අමුතුම සංකේතයකට … 😀 අපි බලමු මොකක්ද ඒ සංකේතය කියලත් එකේ තේරුම මොකක්ද කියලත්… පොඩ්ඩක්වත් අමාරු නැහැ. පොඩ්ඩක්වත් බය වෙන්න ඕනේ නැහැ….

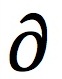
මේ තමයි ආංශික අවකලනයේදී අපිට හම්බෙන සංකේතය.. ඔයාල “ඩාබ” නැත්තම් “ඩබා” කියල කියන්නේ මේ සංකේතයට තමයි 😀 එහෙනම් ඔයාල සංකේතයත් දැනගත්ත නිසා අපි බලමු ශ්‍රිතයක් ආංශික අවකලනය කරද්දී අංකනය කරන්නේ කොහොමද කියල… පොඩ්ඩක්වත් අමාරු නැහැ. නමුත් ඔයාල මේ සංකේත සහ අංකන වල තේරුම අනිවාර්යෙන් මතකයේ තබා ගන්න නම් ඕනේ වෙනවා. එකට අමතර මහන්සියක් වෙන්න ඕනේ නැහැ. ඔයාල ගැටළු හොයාගෙන කරන්න. ඔයාලගේ නිබන්ධන සහ පසුගිය විභාග ප්‍රශ්න හොදටම ප්‍රමාණවත් වෙනවා ඒ කටයුත්තට.

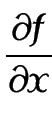
ඔයාල මේ සංකේතය දැකලත් ඇති. මෙයින් අදහස් වෙන්නේ f කියන ශ්‍රිතය x විෂයයෙන් ආංශික අවකලනය කරනවා කියන එකයි.. එම සංකේතය මෙන්න මෙහෙමත් අපිට ලියන්න පුළුවනි…

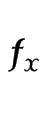
මේ සංකේත දෙකෙන්ම කියන්නේ f කියන ශ්‍රිතය x විෂයයෙන් ආංශික අවකලනය කරනවා යන්නයි… පොඩ්ඩක්වත් අමාරු නැහැ නේද ?
මේ ගමන් මම තව පොඩි දෙයක් කියන්නත් ඕනේ. එක කියලම අපි ඉස්සරහට යමු… ඔයාල dy /dx කියන සංකේතය තේරුම් ගත්තනේ. අපි මේකට කියන්නේ y කියන ශ්‍රිතය x විෂයයෙන් එක් වරක් අවකලනය කිරීමයි. එසේ එක් වරක් අවකලනය කලාම අපි කියනවා පළමුවෙනි ගණයේ අවකලනයක් ( first order differentiation ) කියලා. අපි බලමු කොහොමද දෙවෙනි ගණයේ අවකලනයක් ලියන්නේ කියල ( second order )

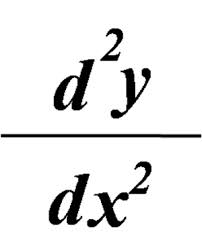
මේ සංකේතයෙන් කියන්නේ y එක් වරක් x විශයෙන් අවකලනය කල පසු ලැබෙන ප්‍රකාශනය නැවතත් x විශයෙන්ම අවකලනය කරනවා කියන අදහසයි.ටිකක් තේරුනේ නැහැ වගේ නේද ? අපි එහෙනම් උදාහරණයක් අරන් බලමු. මම y = 4x +1 කියන ඉතාම සරල උදාහරණයක් ගත්තා ඔයාලට පැහැදිලි කරලා දෙන්න. අපි දැන් මේක එක් වරක් අවකලනය කරමු.දැන් ඔයාල මම මුලින්ම කියල දුන්නු අවකලන නීති නම් මතකයේ තබා ගෙන ඉන්න ඕනි 😀 එහෙනම් dy /dx =4 වෙනවා. නැවතත් මෙය අවකලනය කලවිට උත්තරේ මොකක් කියලද ඔයාල හිතන්නේ ?? මතක නේද මම කිව්වා නියතයක් අවකලනය කලාම උත්තරේ 0 කියල.ඒ කියන්නේ නැවතත් අවකලනය කලවිට පිළිතුර 0 වෙනවා…මොකද 4 කියන්නේ නියතයක් නිසා….ඔයාලට මේවා අමතක නම් ඔයාල ලග තියෙන නිබන්ධන අනිවාර්යෙන්ම කරන්න ඕනේ වෙනවා

අපිට ශ්‍රීතයක් කිහිප වතාවක්ම අවකලනය කරන්න පුළුවන්. ඒ කියන්නේ දෙවෙනි ගණයේ මෙන්ම තුන්වෙනි ගණයේ , සිව්වෙනි ගණයේද අවකලනය තියෙනවා.ගණිතයේදී ඒවාට කියන්නේ ඉහල ගණයේ අවකලනයන් කියලයි (Higher Order Derivatives). ඒවාසංකේතවත් කරන්නේ මෙන්න මෙහෙමයි….ඉතාම පහසුයි…

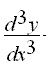
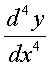
ඒ වගේම ඔයාල අනිවාර්යෙන්ම මතක තියා ගන්න ඕනේ දෙයකුත් තියෙනවා…..

සහ

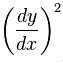
කියන සංකේත දෙක ඔයාල දැක්කනේද? ඔයාලගේ ගොඩක් අයට හිතෙනවා ඇති මේ සංකේත දෙකෙන්ම කියන්නේ එකම දේ කියල. ඒක වැරදියි. ඇත්තෙන්ම මේ සංකේත දෙකෙන් කියවෙන අදහස තෝරලා බේරලා වෙන් කරලා ගත්තම අපිට බලා ගන්න පුළුවන් කොහොමද මේ සංකේත දෙකක් වෙන්නේ කියලා.ඇත්තෙන්ම ඔයාලට ගොඩක්විට පැටලෙන තැනක් මේක, ඒ නිසා අපි පරිස්සමින් මේ සංකේත දෙක හදුනා ගමු නේද?අපි එහෙනම් බලමු පලවෙනි සංකේතයෙන් කියන්නේ මොකක්ද කියල…

පලවෙනි සංකේතයෙන් කියන්නේ y දෙවරක් x විශයෙන් අවකලනය කරනවා කියන එකයි,එහෙමත් නැත්තම් y වල දෙවෙනි ගණයේ අවකලනය තමයි මුල්ම සංකේතයෙන් කියන්නේ..දෙවෙනි සංකේතයෙන් කියන්නේ y එක් වරක් x විශයෙන් අවකලනය කර එහි දෙවෙනි බලය ගන්නා බවයි.දැන් ඔයාලට තේරෙනවා නේද මේ සංකේත දෙකේ වෙනස්කම ? හොදම දේ ඔයාලත් උදාහරණයක් අරන් තනිවම කරලා බලන්න ඕනේ. එතකොට ඔයාලටම තහවුරු කරගන්න පුළුවන් මම කිව්වා දේ 😀

එහෙනම් අපි ඩාබ ලගට යමු නේද? ආංශික අවකලනයේත් දෙවෙනි තුන්වෙනි ගණයේ අවකලන තියෙනවා. අපි බලමු කොහොමද දෙවෙනි ගණයේ ආංශික අවකලනයක් සංකේතවත් කරන්නේ කියලා… හරිම පහසුයි…

අපි මුලින්ම බලමු f කියන ශ්‍රිතය දෙවරක් x විෂයයෙන් ආංශික අවකලනය කිරීම යන්න සංකේතවත් කරන්නේ කොහොමද කියලා

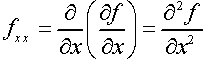
ඊලගට අපි බලමු f කියන ශ්‍රිතය දෙවරක් y විෂයයෙන් ආංශික අවකලනය කිරීම යන්න සංකේතවත් කරන්නේ කොහොමද කියලා

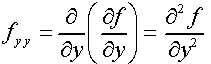
අපි දැන් ඊලගට විශේෂ අවස්ථාවකට යන්න හදන්නේ… ඔයාලට මතක නේද ආංශික අවකලනයක් සිදු කරන්නේ ශ්‍රිතයේ විචල්‍යය එකකට වඩා වැඩිපුර තිබ්බමයි කියලා… එහෙනම් අපිට පුළුවන් ශ්‍රිතයක් පළමුවෙනි වාරයේ x විශයෙන් ආංශික අවකලනය කරලා නැවතත් y විශයෙනුත් ආංශික අවකලනය කරන්න… පොඩ්ඩක් තේරුනේ නැහැ නේද? පොඩ්ඩක්වත් කලබල වෙන්නෙපා.. අපි මුලින්ම සංකේතය හදුනා ගෙන ඉමුකො 😀 ඊට පස්සේ මම උදාහරණයක් අරගෙන පැහැදිලි කරලා දෙන්නම්කො…

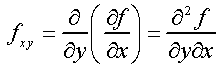
ඒ වගේම අපිට පුළුවනි ශ්‍රිතයක් පළමුවෙනි වාරයේ y විශයෙන් ආංශික අවකලනය කරලා නැවතත් x විශයෙනුත් ආංශික අවකලනය කරන්න…

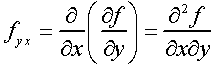
අපි දැන් උදාහරණයක් අරන් බලමු කොහොමද මේව වෙන්නේ කියලා…. 😀

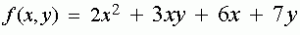
ඔයාලට පේනවා නේද? මේ ශ්‍රිතයේ තියෙන විචල්‍යයන් x සහ y පමණක් බව. අපි එහෙනම් මේ ශ්‍රිතය x විශයෙන් ආංශික අවකලනය කරමු. එතකොට අපිට ලැබෙනවා මෙන්න මෙහෙම දෙයක්…

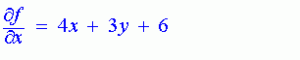
ඔයාල මෙහෙදී මතක තබා ගන්න ඕනේ දෙයකුත් තියෙනවා. අපි මේ උදාහරණයම අරන් බලමුකෝ. දැන් අපි කලින් කලේ ශ්‍රිතය x විශයෙන් ආංශික අවකලනය කිරීමනේ. එතැනදී අනිත් සියලුම විචල්‍යයන් නියතයන් විදිහට සලකනවා. තේරුනේ නැහැ වගේ නේද? අපි එහෙනම් පරිස්සමින් බලමුකෝ කොහොමද එහෙම කරන්නේ කියලා….
අපි උදාහරණයට ගත්තු ශ්‍රිතයේ පද හතරක් තියෙනවා කියලා ඔයාලට පේනවා නේද? පලවෙනි පදය x විශයෙන් අවකලනය කරවිට ලැබෙන්නේ 4x කියන පදයයි,දෙවෙනි පදය x විශයෙන් අවකලනය කරද්දී ඔයාලට පේනවා නේද y ත් එතන තියෙනවා…මම කලින් කිව්වා වගේ දැන් අපි y සලකන්නේ නියතයක් විදිහටයි…ඔයාලට මතකනේද නියතක් සමග ශ්‍රිතයක් ගුණිතයක් විදිහට තිබ්බොත් අවකලනය කරන්නේ කොහොමද කියලා? අන්න ඒ විදිහට අවකලනය කලාම අපිට ලැබෙනවා 3y කියන පදය, තුන්වෙනි පදය x විශයෙන් අවකලනය කලාම ලැබෙන්නේ 6 කියන පදයයි,අවසානයට තියෙන්නේ 7y කියන පදයයි.මේ සම්පුර්ණ පදයම නියතයක් වෙනවා..නියතයක් අවකලනය කලවිට පිළිතුර 0 වෙනවා.දැන් පරිස්සමින් වෙන වෙනම අවකලනය කරපු පද ටික එකතු කලාම ඉහත මම සදහන් කල පිළිතුර ලැබෙනවා.දැන් ඔයාලට තේරුනා නේද.පොඩ්ඩක්වත් අමාරු නැහැ…

අපි තවත් ඉස්සරහට යමුකෝ…දැන් ආයිත් x විශයෙන් ආංශික අවකලනය කරපු ප්‍රකාශනය නැවතත් අපි x විශයෙන් ආංශික අවකලනය කරමු. එතකොට අපිට ලැබෙන්නේ මෙන්න මේ වගේ දෙයක්….

ඔයාලට පේනවා නේද මෙතැනදී නියත පද වෙන්නේ 3y කියන පදයයි 6 කියන පදයයි බව. ඒ නිසා අපිට ඉතිරි වෙන්නේ 4x කියන පදය විතරයි. එම පදයත් x විශයෙන් ආංශික අවකලනය කලාම පිළිතුර 4යි.දැක්ක නේද ඉතාමත් ලේසියි කියලා…

අපි මුල් ශ්‍රිතය y විශයෙන් අංශික අවකලනය කරමු..

ඔයාලට මම මුලින්ම කියල දුන්නනේ x විශයෙන් කොහොමද ආංශික අවකලනය කරන්නේ කියලා,ඒ වගේම කොහොමද අනෙක් විචල්‍යන් නියත විදිහට සලකලා අවකලනය කරන්නේ කියලා..දැන් අපි ශ්‍රිතය y විශයෙන් ආංශික අවකලනය කරනවා නම් නියත විදිහට සලකන්නේ x කියන විචලයයි.මම කලින් කියල දුන්නු පියවරවල් ඉතාමත් පරිස්සමින් අනුගමනය කලාම ඔයාලට ඉහත මම සඳහන් කරපු ප්‍රකාශනය ලබා ගන්න පුළුවනි. පොඩ්ඩක්වත් අමාරු නැහැ.. ඔයාල එක තනිවම කරලා බැලුවොත් හොදයි කියලයි මට හිතෙන්නේ… 😀

අපි දැන් කලින් y විශයෙන් අවකලනය කරපු ශ්‍රිතය නැවතත් y විශයෙන් අවකලනය කලාම ලැබෙන්නේ මොකක්ද කියලා බලමු..

දැන් අපි මම කලින් සඳහන් කරපු විශේෂ අවස්ථා දෙකට යමු.මොකද ඔයාලට තේරුනෙත් නැහැනේ 😀

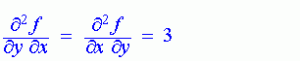
මෙතැනදී මුලින්ම කියන්නේ f කියන ශ්‍රිතය මුලින්ම x විශයෙන් ආංශික අවකලනය කර නැවත y විශයෙන් ආංශික අවකලනය කිරීමයි. එයින් ලැබෙන පිළිතුරත් ශ්‍රිතය මුලින්ම y විශයෙන් ආංශිකව අවකලනය කර නැවත x විශයෙන් ආංශික අවකලනය කලවිටද ලැබෙන පිළිතුරත් එකම වෙන බව ඔයාලට මේ උදාහරණයෙන් පේනවා…

මම දැන් හිතනවා ආංශික අවකලනය ගැන ඔයාලට ලොකු දැනුමක් වගේම මේ කොටස සම්බන්ධයෙන් ගැටළු තිබුණු අයට ඔයාලගේ ගැටළු නිරාකරණය කරගන්න පුළුවන් වුනා කියලා…. ආංශික අවකලනයේ ඔයාලට කියල දෙන්න තියෙන ප්‍රධානම සිද්ධාන්ත ටික මං ඉතාමත් සරලව ඔයාලට කියලා දුන්නා…. නමුත් ගැටළු විසදද්දී මම කලින් වාර වල ඔයාලට කියලා දුන්නු මුලික අවකලන නීති, ත්‍රිකෝණමිතික ශ්‍රිත අවකලනය කරන්නේ කොහොමද, ඒ වගේම දාම නිතිය (chain rule) පාවිච්චි කරන්නත් සිද්ධ වෙනවා ඔයාලට. මම එක තමයි කලින් ලිපියේ සඳහන් කලේ මෙම කරුණු හැම එකක්ම එකිනෙකට සම්බන්ධයි කියලා…. එහෙනම් මම ඊලග වාරයේදී ඔයාලගේ කොක්ක ගැන කියලා දෙනවා. ඒ කියන්නේ අනුකලනයේ මුලික කොටස්, ඔයාල දැනගෙන ඉන්න ඕනේ කොටස් ටික මේ වගේම ඉතාමත්ම සරලව කියලා දෙනවා. අපි ඉක්මනින් ආයිත් මුණගැහෙමු මේ වගේ පාඩමකින්. එහෙනම් කට්ටියටම ජයවේවා!!!!