හ්ම්ම්ම්…ඔයාල දැන් අවකලනය ගැන වගේම ආංශික අවකලනය ගැනත් හොද දැනුමක් ලබා ගත්තනේ පහුගිය ලිපි මාලාවෙන්…එහෙම නේද? එහෙනම් අපි යමු එහෙනම් ඔයාලට ඇණයක් වෙච්ච කොක්ක ලගට…. ඇත්තටම කොක්ක එහෙමත් නැත්තම් අනුකලනය කිසිසේත්ම ඇණයක් නෙමෙයි 😀 ඇත්තෙන්ම ජීව විද්‍යාව සහ අණුක ජීව විද්‍යාව කරන අපේ නංගිලා මල්ලිලාට අනුකලනයේ ගොඩාක් ගැඹුරට ඉගෙන ගන්න දෙයක් නැහැ.අනුකලනයේ මුලිකම සිද්ධාන්ත ටික ඉගෙන ගත්තම හොදටම ඇති…නමුත් ඔයාල අනුකලනය ඉගෙන ගන්නකොට අවකලනය අමතක කරලා නම් ඉන්න බැහැ හොදද? ඒ ඇයි කියල මම පැහැදිලි කරලා දෙන්නම් ඉක්මනින්ම…ඒ වගේම සම්මත අනුකලන කියල කොටසක් තියෙනවා…ඔයාලට මතකනේද මම අවකලනයේ නීති වගේම සම්මත ත්‍රිකෝණමිතික අවකලන ටිකත් මතකයේ තියා ගන්න කිව්වා…එව්වා අමතක නම් මෙන්න මේ link එකෙන් ගිහින් බලන්න පුළුවන් ඔයාලට එහෙනම් ඔයාල ලෑස්තියි නේද අපේ කොක්ක හම්බෙන්න යන්න??? එහෙනම් යමු. 😀 ඇත්තෙන්ම අවකලනයේ ප්‍රතිලෝම ක්‍රියාවලිය ලෙස අනුකලනය ඉතාමත් සරලව හදුන්වන්න පුළුවන්…ඔයාලගේ මට්ටමින් අන්න එහෙම මතක තියාගෙන පොඩි දල අදහසක් ගන්න අනුකලනය කියන්නේ මොකක්ද කියලා…නමුත් අවකලනය වගේම අනුකලනයත් ඉතාම ගැඹුරු ගණිත සංකල්පයක්.එහෙනම් අපි දැන් අනුකලනය කියන්නේ මොකක්ද කියල දැනගත්තානේ.ඔයාලට මතක නේද අවකලනයේ ජ්‍යාමිතික අර්ථ දැක්වීමක් මම ඔයාලට කියල දුන්නා.ඔයාලට අමතක නම් මෙන්න මේ link එකෙන් ගිහින් බලන්න පුළුවන් පහසුවෙන්ම ඒ කියන්නේ xy ඛණ්ඩාංක තලයේ අදින ඕනෑම වක්‍රයක බෑවුම තමයි අවකලන සංගුනකයෙන් අදහස් වෙන්නේ.ඒ වගේම අනුකලනය කියන්නේ සන්තතික (continuous) එකතු කිරීමක් ලෙසට අපිට ජ්‍යාමිතිකව හදුනවා දෙන්න පුළුවන් ඉතාමත් සරල ආකාරයකට.ඔයාලට ඒ සම්බන්දයෙන් ගැඹුරට ඉගෙන ගන්න දෙයක් නැහැ.නමුත් ඛණ්ඩාංක තලයේ අනුකලනයෙන් ගන්න ලොකුම ප්‍රයෝජනය තමයි වක්‍රයක් යට වර්ගඵලය සෙවීම.පහත රුපයෙන් ඔයාලට එක හොදටම පැහැදිලි කරගන්න පුළුවන්..

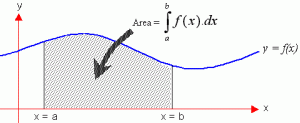
මෙතන y=f(x) කියල ශ්‍රිතයක වක්‍රය තමයි නිරුපනය වෙන්නේ.ඒ වගේම x=a වල ඉදන් x=b වෙනකන් සිමාවේ (limit) එම වක්‍රය සහ x අක්ෂය සමග ඇති අවකාශයේ වර්ගඵලය තමයි හොයලා තියෙන්නේ…දැන් මම හිතනවා ඔයාලට වක්‍රයක් යට වර්ගඵලය හොයන්නේ කොහොමද කියලා..මම අනුකලනයේ ජ්‍යාමිතික භාවිතයක් ගැන ඔයාලට කියලා දුන්නේ ඔයාලට අනුකලනය ගැන අවබෝධයක් ලබා දෙන්න… ඔයාල වස්තුවක ගුරුත්ව කේන්ද්‍රය (center of gravity) ගැන අහල ඇති නේද? එහෙමත් නැත්තම් ස්කන්ධ කේන්ද්‍රය ගැන (center of mass)… ඔයාල උසස් පෙළ කාලයේ භෞතික විද්‍යාවට සම්මත වස්තු වල ගුරුත්ව කේන්ද්‍ර ගැන ඉගෙන ගත්තා මතක ඇති. 😀 ඒ වගේම සම්මත වස්තු වල අවස්ථිති ඝුර්ණය (moment of inertia) ගැනත් අහල ඇතිනේ උසස් පෙළ කාලයේ? ඔයාල දැනන් හිටියාද ඒ සියලුම දේවල් කලේ අනුකලනයෙන් බව ???? ඒ කියන්නේ අනුකලනයෙන් සෑහෙන්න දේවල් කරන්න පුළුවන් ගණිතයේදී. මම මේ උදාහරණ ඔයාලට කිව්වේ ඔයාල බලනවා ඇති මම මේ අනුකලනය කියල දෙනවා.. අනුකලනයෙන් මොකක්ද කරන්න පුළුවන් දේ? නිකන්ම නිකන් ගණිත කර්මයක් වෙන්න ඇති කියල… 😀 මම දන්නවා ඔයාල ගොඩක් අය එහෙම හිතන්න ඇති කියලා…එහෙනම් දැන් ඒ සැකෙත් නැති වුනානේ.එහෙනම් අපි යමු අනුකලනයේ සිද්ධාන්ත කොටස් වලට.පොඩ්ඩක්වත් අමාරු නැහැ.අපි හිමිහිට යමු අපේ කොක්ක ලගට. ඔයාල දැනගන්න ඕනේ ප්‍රධාන අනුකලන වර්ග දෙකක් තියෙනවා.

1. අනිශ්චිත අනුකල
2. නිශ්චිත අනුකල

මොකක්ද මේ අනිශ්චිත අනුකල (indefinite integral) කියන්නේ? නිශ්චිත අනුකල (definite integral) කියන්නේ මොකක්ද? ගොඩක් අයට පැටලෙන තැනක් මේක…මම මගේ පාඩමෙන් මේ ගමන කියලා දෙන්නේ අනිශ්චිත අනුකල ගැනයි..මගේ ඊලග පාඩමෙන් නිශ්චිත අනුකල ගැන ඔයාලට කියල දෙනවා…ඇත්තෙන්ම මොකක්ද මේ නිශ්චිත අනුකල කියන්නේ??අපි ඊට කලින් බලමු අනිශ්චිත අනුකලනයක් සංකේතවත් කරන්නේ කොහොමද කියල…

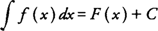
අපි බලමු මේ ප්‍රකාශනයෙන් කියන්නේ මොකක්ද කියලා.f(x) කියන ශ්‍රිතය x විෂයයෙන් අනුකලනය කරනවා කියන එක තමයි වම් අත පැත්තෙන් කියන්නේ.දකුණු අත පැත්තෙන් කියන්නේ f(x) කියන ශ්‍රිතය x විෂයයෙන් අනුකලනය කල විට ලැබෙන්නේ F(x) ශ්‍රිතය සහ C යන්න බවයි.ඔයාලට F(X) ගැන නම් ප්‍රශ්නයක් නැතිවෙයි…ප්‍රශ්නයක් එනවා ඇති මෙන්න මේ C ගැන. මොකක්ද මේ C????? අපි C ව හදුන්වනවා අනුකල නියතය (integration constant) එහෙමත් නැත්තම් අභිමත නියතය (arbitrary constant) විදිහට…දැන් ඔයාලට ප්‍රශ්නයක් එනවා ඇති කොහෙන්ද එක පාරටම මේ අනුකල නියතය කඩා පාත් වුනේ කියලා… 😀 ඔයාලට මතක ඇති මම කිව්වා නියතක් අවකලනය කලාම උත්තරේ 0 කියලා..එහෙනම් 0 කියන අගය අනුකලනය කල විට ලැබෙන්නේ නියතයක්, මොකද අනුකලනය කියන්නේ අවකලනයේ ප්‍රතිලෝම ක්‍රියාවලිය නිසා…දැන් මම හිතනවා ඔයාලට හොදටම තේරෙන්න ඇති කියලා මේ අනුකල නියතය ගැන වගේම ඒක කොහොමද සම්බන්ධ වෙන්නේ කියලා… ඒ වගේ අනුකල නියත යෙදෙන අනුකලන වලට තමයි අනිශ්චිත අනුකල කියන්නේ.අපිට ඒ අනුකල නියතය හොයන්නත් පුළුවන්.අපිට එකට අමතර දත්ත ලබා දෙන්න වෙනවා.නමුත් ජීව විද්‍යාව සහ අණුක ජීව විද්‍යාව කරන නංගිලාට සහ මල්ලිලාට ඒ තරම් ගැටළු විසදන්න හම්බෙන එකක් නැහැ.නමුත් පොඩ්ඩක්වත් අමාරුත් නැහැ 😀 එහෙනම් ඔයාලට තේරෙනවා ඇති නේද මම නොකිව්වත් නිශ්චිත අනුකල කියන්නේ මොකක්ද කියලා??? නිශ්චිත අනුකල වලදී කලින් වගේ අනුකල නියතයක් එන්නේ නැහැ..දැන් ඔයාලට ප්‍රශ්නයක්…කොහොමද එහෙම වෙන්නේ???? එකට මම උත්තරේ දෙන්නම් මෙන්න මෙහෙම.. පල්ලෙහා තියෙන රුපය හොදට අධ්‍යනය කරන්නකෝ 😀

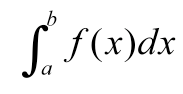
මේ සංකේතයෙන් කියන්නේ f(x)කියන ශ්‍රිතය a සහ b කියන සීමාව ඇතුලෙදි x විශයෙන් අනුකලනය කරනවා යන්නයි.අපි හිතමු f(x) කියන ශ්‍රිතය අනුකලනය කලවිට ලැබෙන්නේ F(x) කියන ශ්‍රිතය කියලා එතකොට අපි ලියන්නේ මෙන්න මෙහෙමයි…

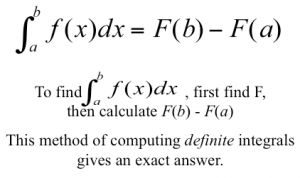
අපි නිශ්චිත අනුකල කරන්නේ කොහොමද කියලා අපේ ඊලග පාඩම් වලින් බලමු.අද අපි අනිශ්චිත අනුකල වල මුලික කොටස් ඉගෙන ගනිමු.මේ නම් ඇහුවම ටිකක් බයයි වගේ නේද? බය වෙන්න දෙයක් නැහැ.ඔයාලට හුරු වෙද්දී බය නිකන්ම ඇරිලා යාවි. 😀 ඔයාල මෙන්න මේ සම්මත අනුකල නම් මතක තියා ගන්න ඕනේ වෙනවා.අපි එහෙනම් “අ” යන්නෙන් පටන් ගමු හිමිහිට… 😀 අපි මුලින්ම මුලික අනුකලන නීති ගැන හොයල බලමු…ඕ ඕ ඔයාල මතක තියා ගන්න ඕනේ මේ සම්මත අනුකල වගේම අනුකල නීති, අනිශ්චිත අනුකල වලට මෙන්ම නිශ්චිත අනුකල වලටද එකසේ පිළිපැදිය යුතු බව…. පලවෙනි නීතියෙන් කියන්නේ නියතයක් අනුකලනය කිරීමයි.ඔයාලට අවකලනයේදී මම කිව්වා මතක ඇති d (ax)/dx = a කියලා…එහෙනම් අනුකලනයේදී වෙන්නේ එකේ අනිත් පැත්ත…ඒ කියන්නේ a කියන නියතය (constant) අනුකලනය කලොත් හම්බෙන්නේ ax කියන ශ්‍රිතයයි.මීට අමතරව c කියන්නේ අනුකල නියතය බව දැන් ඔයාල හොදින්ම දන්නා කාරණයක්…

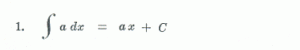
දෙවෙනි නීතියෙන් කියන්නේ ශ්‍රිත දෙකක් එකතුවකින් බැදිලා තියෙන විට ඒ කියන්නේ u(x) + v(x) වගේ තියෙනකොට අපිට අවකලනයේදී වගේම අනුකලනයේදීත් කොටස් කරලා අනුකලනය කරන්න පුළුවන් කියන එකයි.මෙහෙදී ඔයාල මතකයේ තියා ගන්න ඕනේ u සහ v කියන්නේ x වල ශ්‍රිත කියලා…ඒ වගේම මේ නීතිය ශ්‍රිත දෙක අන්තරයකින් තියෙන කොටත් පාවිච්චි කරන්න පුළුවන්.ඒ කියන්නේ u(x) – v(x) වගේ අවස්ථාවකදී…එකත් ඔයාල හොදට සිහියේ තියා ගන්න ඕනේ…

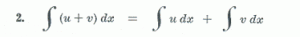
තුන්වෙනි නීතියෙන් කියන්නේ අනුකලනය කල යුතු ශ්‍රිතය නියතයක් සමග ගුනිතයකින් බැඳී තියෙනකොට අපිට නියතය අනුකලනයෙන් පිටතට අරගෙන අදාළ ශ්‍රිතය අනුකලනය කරන්න පුළුවන් කියන එකයි… ඔයාලට මතක නම් මම අවකලනයේදීත් මීට සමාන නීතියක් කිව්වා මතක් වෙන්න ඕනේ 😀

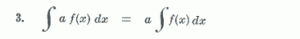
දැන් අපි මුලික නීති දැනගත්තානේ..එහෙනම් අපි බලමු සම්මත අනුකල කොහොමද වෙන්නේ කියලා…පහත රූප සටහනේ වම් පැත්තේ ශ්‍රිතයේ අවකලනයත්, දකුණු පැත්තේ ඊට අදාළ අනුකලනයත් දැක්වෙනවා.පොඩ්ඩක්වත් අමාරු නැහැ..නමුත් මතකයේ තබා ගන්න ඕනේ ඔයාල.කිසිම අමාරුවක් නැහැ එකටත්.. 😀 ඔයාල ලග තියෙන නිබන්ධන සහ පසුගිය ප්‍රශ්න පත්‍ර හොදටම ප්‍රමාණවත්… n කියලා කියන්නේ ඕනෑම ධන හෝ ඍණ සංඛ්‍යාවක් විටදී (n0 විටදී);

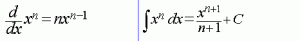
නමුත් ඔයාල මතක තියා ගන්න ඕනේ මේ අනුකලනය n=-1 අවස්ථාවට අදාළ වෙන්නේ නැති බව…මොකද n=-1 විටදී ශ්‍රිතය 1/x බවට පත් වෙනවා.ඒ අවස්ථාවට වෙනම අනුකලනයක් තියෙනවා…. එක ලියන්නේ මෙන්න මෙහෙමයි….

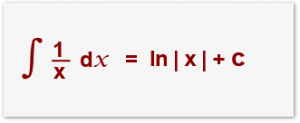
ඔයාල එකත් හොදට සිහියේ තියා ගන්න ඕනේ හොඳද??? අපි දැන් එහෙනම් ත්‍රිකෝණමිතික ශ්‍රිත අනුකලනය කරන්නේ කොහොමද කියලා බලමු..

මේ වගුවේ csc x කියල කියන්නේ cosec x කියන ශ්‍රිතයයි…මම මේ බව ඔයාලට මගේ දෙවෙනි පාඩමෙන් කිව්වා මතක ඇති නේද? 😀 ඔයාල මේ සම්මත ත්‍රිකෝණමිතික ශ්‍රිත අනුකලනය කරන හැටි මතකයේ තියා ගන්න ඕනේ.මම අවකලනයත් එක්ක සංසන්දනය කරලා ඔයාලට අනුකලනය කරන්නේ කොහොමද කියලා පෙන්නුවේ ඔයාලට පහසුවෙන්ම මතකයේ තියා ගන්නයි… අපිට තවත් ශ්‍රිතයක් තියෙනවා අනුකලනය කරන්න.අපි බලමු ඒ මොකක්ද කියලා…

මේ තමයි ඝාතීය ශ්‍රිතය (exponential function)

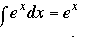
මෙම අනුකලනය ඍණ අවස්තාවටත් ගැලපෙනවා.

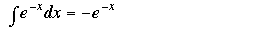
a කියලා කියන්නේ ඕනෑම ධන හෝ ඍණ නියතයක් විට අපිට මම මුලින් සඳහන් කරපු අවස්ථා දෙකම පොදුවේ පහත පරිදි ලියන්න පුළුවන්….

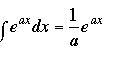
මෙව්වා තමයි මුලික අනුකලන ටික… නමුත් තවත් සම්මත අනුකලන තියෙනවා…එව්වා ඔයාලට අවශ්‍ය වන්නේ නැහැ… 😀 මේ කියල දීපු එව්වත් පොඩ්ඩක්වත් අමාරු නැහැ… 😀 එහෙනම් ඉතාමත් දීර්ඝ අනුකලන පාඩමක් මම ඉවර කරන්නයි හදන්නේ…මම මගේ මීලග පාඩමෙන් ඔයාලට කලින් පොරොන්දු වුනා වගේ නිශ්චිත අනුකල ගැන ඉතාමත් සරලව කියලා දෙනවා…ඒ වගේම තවත් දෙයක් කියන්න තියෙනවා…මගේ කොක්ක පාඩම දැන් ටික ටික අවසානයට ලං වෙනවා…ලබන පාඩමේදී අලුත් දේවල් කියලා දෙනකොට අද මම කියපුවා නම් ඔයාල අනිවාර්යෙන්ම මතකයේ තියා ගන්න ඕනේ වෙනවා..එහෙනම් අපි ඉක්මනින්ම ඊලග පාඩමෙන් මුණ ගැහෙමු.ඔයාල හැමෝටම ජය වේවා!!!!!

Image sources :
http://www.teacherschoice.com.au
http://www.cliffsnotes.com
http://www.solitaryroad.com
http://www.cobalt.chem.ucalgary.ca
http://mathematicsi.com
http://www2.bc.cc.ca.us
http://drphilsmathvideos.com