ඔබ මොහොතකට රාත්‍රී කාලයේ නිවසෙන් බැහැරට පැමිණ අහස දෙස බැලූ විට දකින්නට ලැබෙන්නේ කුමක්ද?මිහිඳුම් හෝ වැහිබර අහසක් නොවේ නම් එහිදී අවම වශයෙන් තාරකා එකක් දෙකක් හෝ සහිත අහසක් දක්නට ලැබෙනු ඇත. මෙකී තාරකා විවිධ වර්ණවලින් දිදුලනු දක්නට ලැබෙනු ඇත.එකී තාරකා පිලිබඳ සොයා බැලීමට ඕනැම කෙනෙකු පෙළඹෙන්නේ නිතැතිනි.

අහසේ තරු පිළිබඳ පුරාතනයේ සිටම මිනිසා දැක්වූයේ විශාල සැලකිල්ලකි. එය දේවත්වයේ සිට ශක්ති ප්‍රභවයක් නම් වූ විද්‍යාත්මක ඇසින් දැක්ම දක්වා කාලයත් සමග වෙනස් වූ මිනිස් දැක්ම තුලින් තමන්ගේ බොහෝ ගැටළු වලට පිලිතුරු ඇතැයි විශ්වාස කරයි. විශේෂයෙන් විශ්වයේ ව්‍යප්තිය, ජීවයේ ප්‍රභවය, විශ්වයේ ක්‍රියාවන්හි පෘථිවියට වන බලපෑම ඒ අතරින් විශේෂය. ඒ අනුව තාරකාවල ගුණාගුණ අධ්‍යයනය වර්තමාන තාරකා විද්‍යාවේ ප්‍රධාන අංගයක් වී ඇත. ඒ සඳහා තාරකාවක ප්‍රමාණාත්මක ගුණ අධ්‍යයනය උදෙසා තාරකා වලට අදාල භෞතික පරාමිතින් කිහිපයක් පවතින අතර ඒවා පහත පරිදි වේ.

1. දුර
2. දීප්තිය
3. උෂ්ණත්වය
4. අරය
5. ස්කන්ධය
6. වයස
7. රසායනික සංයුතිය

මෙකී පරාමිතින් ලබා ගැනීම සඳහා පහත මිනුම් ලබා ගැනීම සිදු කරන අතර මේවා හරහා සෘජු හෝ වක්‍ර ලෙස තාරකවන්හි ඉහත කී පරාමිතින් ලබා ගැනීම සිදු කෙරේ.

• තාරකවේ පිහිටුම
• විවිධ වර්ණාවලි ප්‍රාන්ත වල ස්‍රාවයන්
• වර්ණාවලිය
• විවිධ කාල ප්‍රාන්තවල ඉහත මිනුම් වාර්තා
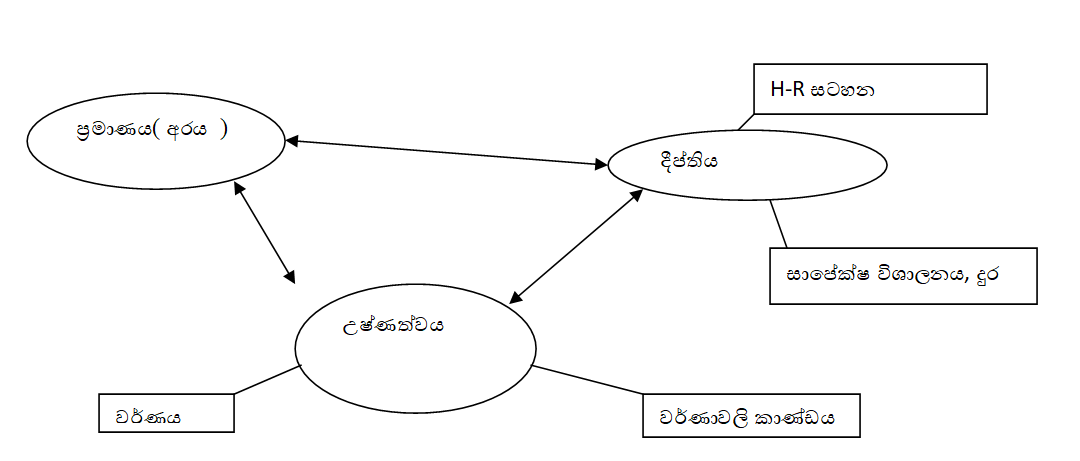
  මෙකී මිනුම් හරහා තාරකාවේ අනිකුත් ගුණාංග අධ්‍යයනය කරනු ලබන අතර මෙකී මිනුම් දඬු අනිකුත් ගුණාංග හා එකිනෙකා හා සම්බන්ධව ඇති අයුරු පහත දැක්වේ.

මේ අනුව තාරකාවේ පිහිටීම (දුර, චලිතය ) පිලිබද මිනුම අතිශය වැදගත් මිනුමක් බව පැහැදිලි  වන අතර මෙම පිහිටීම් සම්බන්ධව මිනුම් ගැනීම නක්ෂත්‍රමිතිය(Astromerty) නමින් හැඳින්වේ.

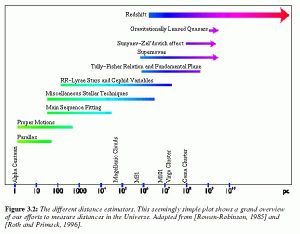
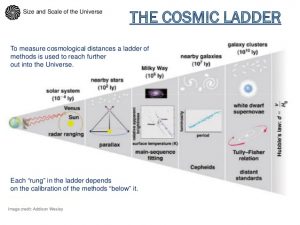
Cosmic Distance Ladder

මෙම ඉණිමග හරහා තාරකාවකට පොලොවේ සිට පවතින දුර සෙවීමේ ක්‍රමවේදයන් පැහැදිලි කරනු ලබන අතර එක් එක් දුර ප්‍රාන්තයන් සදහා වඩා උචිත ක්‍රමවේදය පිලිබදව පැහැදිලි කිරීමක් දක්වයි. මෙකී ඉණිමගේ විශේෂත්වය ලෙස එක් ක්‍රමවේදයකින් අනික් ක්‍රමවේදයන් අනුක්‍රමිකව රැඳීමයි.උදාහරණයක් ලෙස අසම්පාත ක්‍රමවේදය මහින් දුර සොයා ගුණාංග අධ්‍යයනය කරන ලද තාරකාවකට සමාන ගතිගුණ ඇති  තාරකාවකට ඇති දුර සෙවීමට ආලෝකයේ ප්‍රතිලෝම වර්ග නියමය යොදා ගැනීමයි.මෙහිදී පලමු තාරකාවේ ගතිගුණ (දීප්තිය ) අධ්‍යයනයෙන් තොරව දෙවන තාරකාවට ඇති දුර සොයා ගත නොහැකි වන අතර පළමු තාරකාවට දුර සෙවීමෙන් තොරව එහි ගතිගුණ අධ්‍යයනය කළ නොහැක.මේ අනුව එක් මිනුම් ක්‍රමයක් අනික මත රඳා පවතින බව පෙනී යයි.

මේ අනුව තාරාකවක දුර මැනීමට භාවිතා කරන  මූලික මිනුම් ක්‍රමවේදය වන අසම්පාත  ක්‍රමය ගැන සලකා බලමු.

අසම්පාත ක්‍රමවේදය (Parallax)

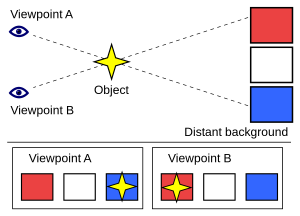
යම් වස්තුවක් එකිනෙකට වෙනස් පිහිටුම් දෙකකින් නිරීක්ෂණය කරන විට එකී වස්තුව දර්ශනය වන පිහිටුම් වල වෙනස් වීම අසම්පාතය ලෙස හඳුන්වයි. මෙය මිනුම් විද්‍යාවේදි දෝෂයක් ලෙස ගැනෙනා අතර මෙය වස්තුවක නිරීක්ෂණය කරන පිහිටුම මත දෘශ්‍ය විස්ථාපනය ලෙස ද ගැනේ.

මෙකී ක්‍රමවේදය හරහා තාරකාවකට ඇති දුර සෘජුව මැන ගත හැකි හෙයින් සෘජු මිනුම් කාණ්ඩයක් ලෙස අසම්පාත ක්‍රමය තාරකා විද්‍යාවේ සැලකේ.

තාරකා විද්‍යාවේ අසම්පාත ක්‍රමයන් කීපයක් පවතින අතර ඒවා පහත පරිදි වේ.

1.  ත්‍රිකෝණමිතික අසම්පාතනය (Trigonometric parallax)
2. විලම්භික අසම්පාතනය (Secular Parallax)
3. සංඛ්‍යානමය අසම්පාතනය (Statistical Parallax)
4. විස්තාරණ අසම්පාතනය (Expansion Parallax)

ත්‍රිකෝණමිතික අසම්පාතනය

මෙකී ක්‍රමවේදය තාරකා විද්‍යාවේ ඉහළ තත්ත්වකරණය සහිත මිනුම් ක්‍රමවේදයක් වන අතර මෙහි ආකාර දෙකකි.

1. පෘථිවි කේන්ද්‍රිය අසම්පාතනය

2. සූර්ය කේන්ද්‍රිය අසම්පාතනය

මෙකී ක්‍රමවේදයන් දෙකෙහිම කේන්ද්‍රය ලෙස සලකන වස්තුව/ලක්ෂ්‍යය හා මිනුම ලබා ගන්න වස්තුව අතර ලම්භකයක් නිර්මාණය කරන අතර, එකී ලම්භකයත්, මිනුම් ලබා ගන්නා වස්තුව හා නිරීක්ෂකයා අතර රේඛාවත් අතර කෝණය මෙහිදී අසම්පාත කෝණය ලෙස ගැනේ.

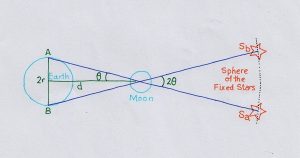
පෘථිවි කේන්ද්‍රිය අසම්පාතනය(Geo–Centric Parallax)

පෘථිවිය මත විෂ්කම්භයක දෙකෙලවර පිහිටුම් දෙකක සිට පෘථිවියට ආසන්න වස්තුවක පිහිටුම සෙවීම සිදුවේ. එකී පිහිටුම් දෙක අතර පවතින දුර වෙනස නිසා ආසන්න ආකාශ වස්තූන් එකිනෙකට වෙනස් කෝණ දෙකකින් දර්ශනය වේ. එකී කෝණ වෙනස යොදා ගනිමින් ත්‍රිකෝණමිතික සම්බන්ධයක් හරහා අදාල වස්තුවට ඇති දුර සොයා ගනු ලැබේ.

tanθ=පෘථිවියේ අරය/පෘථිවියේ සිට අදාල වස්තුවට ඇති දුර

ඉහත ක්‍රියාවලිය හරහා තාරකාවන්ට පවතින දුර සොයා ගත නොහැකි අතර සූර්යයා, චන්ද්‍රයා, අඟහරු වැනි වස්තූන්ට දුර සොයා ගැනීමට මෙය භාවිතා කරයි. තාරකා වලින් ඇතිවන අසම්පාතය මෙහිදී නොමැනිය හැකි තරම් බැවින් මෙකී ක්‍රමය තාරකා වලට දුර සෙවීමට යොදා නොගනී.

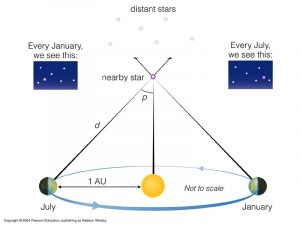
සූර්ය කේන්ද්‍රිය අසම්පාතය(Helio –Centric Parallax)

පෘථිවිය පරිභ්‍රමණය වන පථයේ එහි එකිනෙකට ප්‍රතිවිරුද්ධ  පිහිටුම් දෙකක එනම් අනුයාත මාස හයක පිහිටුම් දෙකකදී තාරකාවක දෘශ්‍ය පිහිටුම් වෙනස ඇසුරින් නිර්මාණය වන අසම්පාතය හරහා එකී තාරකාවට ඇති දුර ත්‍රිකෝණමිතිය ඇසුරින් සොයා ගැනීම මෙනම් වේ.

tanθ=පෘථිවියේ සිට සූර්යයාට ඇති දුර(cm)/පෘථිවියේ සිට අදාල තාරකාවට ඇති දුර(cm)

කුඩා කෝණ සදහා,

tanθ≈θ_rad(රේඩියන)                                  1 rad=648000/Π(විකලා)

θ_rad =පෘථිවියේ සිට සූර්යයාට ඇති දුර(cm)/පෘථිවියේ සිට අදාල තාරකාවට ඇති දුර(cm)

එවිට විකලා(අංශක 3600න් එකක්) එකක් සදහා මෙකී සමීකරණය මෙලෙස විකරණය වේ.

D(පෘථිවියේ සිට අදාල තාරකාවට ඇති දුර)=(648000/Π)×1 AU×10⁵ cm     1 AU=149.60×10⁶ km (පෘථිවියේ සිට සූර්යයාට ඇති දුර)

D=1 Parsec

ඒ අනුව,

D=1/p

මෙහිදී කෝණය p  විකලා(arcsec) වලින් ගත්විට හා පෘථිවිය හා සූර්යයා අතර දුර නක්ෂත්‍ර ඒකක 1 ලෙස ගත් විට අවසානයේ තාරකාවට ඇති දුර පා(ර්)සෙක් (Parsec) වලින් ලැබෙන අතර, පා(ර්)සෙක් එකක අගය ආලෝක වර්ෂ 3.26 කි. මෙහිදී   අදාල තරුව තෙක්  දිවෙන නිර්මාණාත්මක ලම්භකය සූර්යයා කේන්ද්‍ර කර සිදුවෙන බැවින් පෙරකී නාමය භාවිතා වේ.

කෙසේ වෙතත් තාරකා වල අසම්පාතයන් ඉතා කුඩා හෙයින් මෙකී මිනුම් වල නිරවද්‍යතාවයේ සීමා පවතී. පෘථිවිය මත දී එහි වායුගෝලයේ බලපෑම් නිසා අසම්පාත මිනුම 0.05” වඩා විශාල කෝණයන් සදහා නිරවද්‍ය වන අතර, අභ්‍යවකාශයේ ඇති හිපාකස් චන්ද්‍රිකාවේ අසම්පාත කුඩා මිනුම 0.005” වේ. ප්‍රථම ත්‍රිකෝණමිතික අසම්පාතනය ෆෙඩ්‍රික් විල්හෙල්ම් බෙසෙල්( Friedrich Wilhelm Bessel (1784-1846)) විසින් 61සිග්නි(61 Cygni) තාරකාවට සිදු කරන ලද අතර අද එය ආලෝක වර්ෂ 100 ක සීමාවක් තුල පවතින තාරකවන්හි දුර මැනීමට යොදා ගනී.

අසම්පාත ක්‍රමවේදයේ අනිකුත් ක්‍රමවේදයන් පිලිබදව ඊලඟ ලිපියේදී සාකච්ඡා කරමු.

Sources:

https://www.e-education.psu.edu/astro801/content/l4_p3.html
http://www.astro.ucla.edu/~wright/distance.htm
https://phys.libretexts.org/Bookshelves/Supplemental_Modules_(Physics)/Astronomy_and_Cosmology/Cosmology/Michael_Richmond/3._Heliocentric_parallax
http://web.mit.edu/knazemi/www/beginnerExperiment1.htm
http://eaae.ens-lyon.fr/groupspace/METER/activities/the-triangulation-and-parallax-methods.pdf

Image Courtesy:

www.astro.puc.cl
https://www.cfcpoland.com/galery/cosmic-ladder.html
eclass.uoa.gr
http://web.mit.edu/knazemi/www/beginnerExperiment1.htm
https://biologyofbehavior.wordpress.com/2013/09/15/