Historical flow of denumerable sets and cardinality
Before discussing the denumerability of a set we should know how the idea of denumerability came into being. As we have seen in many areas of mathematics, the idea of denumerability also came from a series of questions. First, we will thoroughly discuss those series of questions.
- The Idea of “Limits”
There was a problem using terms like ‘infinitely large’ and ‘infinitely small’ quantities which were essential for Newton’s fluxions and Leibniz’s calculus.
His concept of a fluxion required him to look at the ratio of two quantities and then to determine what happened to this ratio as both quantities simultaneously moved toward zero. In modern terminology, he was describing the limit of the ratio of these quantities, although he used the somewhat more colorful term “ultimate ratio. “
– Journey through Genius Chapter 11
This was the initial idea of limit. But by 1821 Louis Cauchy came up with a term limit and a definition.
When the values successively attributed to a particular variable approach indefinitely a fixed value, so, as to end by differing from it by as little as one wishes, this latter is called the limit of all the others.
– Journey through Genius Chapter 11
But this definition seems a bit wordy so it is not certain about using some words like ‘indefinitely’. The German mathematician Karl Weistrass and his band of disciples gave us the modern-day using epsilon-delta definition of limits.
- Weight between rational and irrational numbers
The idea of limits brought the idea of ‘continuity’ itself.
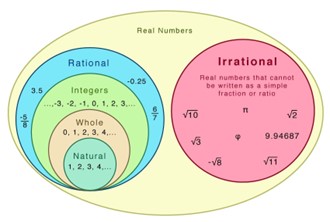
Consider the real number line. It contains rational and irrational numbers. It can be shown that any two distinct rational numbers contain infinite irrational numbers between them and vice versa.
This generally proceeds us to think that rational numbers and irrational numbers are equally distributed.
But in the 19th century using definitions of limits and continuity it was shown that there is a function that is continuous at every irrational point and discontinuous at every rational point, but there is no function that is continuous at every rational point and discontinuous at every irrational point. This suggests that there is no symmetry between rational numbers and irrational numbers.
- Sets Theory
Although mathematicians made huge discoveries in Calculus upon more basic notation of ‘limits’, they got to realize the most important and fundamental questions that were kept rest in calculus profound properties of sets.
These problems were tackled using the ‘set theory’ by George Ferdinand Cantor.
- Comparing the sizes of two infinite sets
In this theory, he came up with an idea about two infinite sets with different sizes.
Infinity is something beyond the counting limit. So obviously we can’t compare 2 infinite sets by counting.
Consider an audience sitting in an auditorium. We can know whether the audience can be seated by counting the number of seats and the number of people in the audience.
Or else, we can ask the audience to be seated and see whether the auditorium fills. Either way we can find the sizes of the two sets are equal.
Similarly in infinite sets even though we can not count the sets we can find whether there exists a one-to-one correspondence between these two sets. If there exists such a correspondence that means those two sets are equal in size.
One-to-one correspondence – This is something like a bijective function combining the two sets. (On to and one-to-one relation)
Definition of a Denumerable set.
We know that set of natural numbers is an infinite set. If another infinite set has the ‘same size’ as the natural number set, then that set is known as a denumerable set.
That means a set having a one-to-one correspondence with the natural number set. In other words, we may be able to create a bijective mapping between Natural numbers and the set if that given set is denumerable.
Example: –
Consider set f(n) = {2n: n ϵ N} Clearly this is an infinite set.
And there is the following one-to-one correspondence between f(n) and natural numbers.
So the set of even numbers is an example of a denumerable set.
Some examples of Denumerable Sets
- Z, set of integers
In order to show the set is denumerable, we must find a function(mapping) that is bijective between natural numbers and integers.
Consider the following mapping 𝑓(𝑛: ℕ ⇒ ℤ).
𝑛/2 𝑛 ∈ ℕ 𝑎𝑛𝑑 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
𝑓(𝑛) = {(n-1)/-2} 𝑛 ∈ ℕ 𝑎𝑛𝑑 𝑛 𝑖𝑠 𝑜𝑑𝑑
The function defined on the domain ℕ and for each 𝑛 ∈ ℕ there exists a
unique 𝑓(𝑛) ∈ ℤ
When 𝑛 ∈ ℕ 𝑎𝑛𝑑 𝑒𝑣𝑒𝑛 f(n)= 𝑛/2 gives ℤ+
When 𝑛 ∈ ℕ 𝑎𝑛𝑑 𝑜𝑑𝑑 f(n)= (𝑛−1)/-2 gives ℤ0−
That means Range(f) = ℤ+ ∪ ℤ0− = ℤ
Range(f)=Codomain(f) means f is subjective.
Let 𝑥1 𝑎𝑛𝑑 𝑥2 be two elements in ℕ
Suppose 𝑓(𝑥1) = 𝑓(𝑥2) = 𝑡 ; 𝑡 ∈ 𝐸
If 𝑡 > 0,
𝑥1/2 = 𝑥2/2 𝑦𝑖𝑒𝑙𝑑𝑠 𝑥1 = 𝑥2
If 𝑡 ≤ 0,
[𝑥1 − 1]/-2 = [𝑥2 − 1]/-2 𝑦𝑖𝑒𝑙𝑑𝑠 𝑥1 = 𝑥2
Either way 𝑓(𝑥1) = 𝑓(𝑥2) ⇒ 𝑥1 = 𝑥2
Therefore 𝑓 is injective.
So 𝑓(𝑛: ℕ ⇒ ℤ) is a bijective mapping between ℤ 𝑎𝑛𝑑 ℕ
So infinite set ℤ is denumerable.
- E = {2,4,6,……} (Set of even numbers)
In order to show the set is denumerable, we must find a function(mapping) that is bijective between natural numbers and integers.
Consider the following mapping 𝑓(𝑛: ℕ ⇒ 𝐸𝑣𝑒𝑛 𝑛𝑢𝑚𝑏𝑒𝑟𝑠).
𝑓(𝑛) = 2𝑛 ; 𝑛 ∈ ℕ
The function defined on the domain ℕ and for each 𝑛 ∈ ℕ there exists a unique 𝑓(𝑛) ∈ 𝐸𝑣𝑒𝑛 𝑛𝑢𝑚𝑏𝑒𝑟𝑠
When 𝑛 ∈ ℕ f(n)=2n gives E (set of all even numbers)
That means Range(f) = E
Range(f)=Codomain(f) means f is surjective.
Let 𝑥1 𝑎𝑛𝑑 𝑥2 be two elements in ℕ
Suppose 𝑓(𝑥1) = 𝑓(𝑥2) = 𝑡 ; 𝑡 ∈ 𝐸
2𝑥1 = 2𝑥2 𝑦𝑖𝑒𝑙𝑑𝑠 𝑥1 = 𝑥2
𝑓(𝑥1) = 𝑓(𝑥2) ⇒ 𝑥1 = 𝑥2
Therefore 𝑓 is injective.
So 𝑓(𝑛: ℕ ⇒ 𝐸) is a bijective mapping between 𝐸 𝑎𝑛𝑑 ℕ
So infinite set 𝐸 (𝑒𝑣𝑒𝑛 𝑛𝑢𝑚𝑏𝑒𝑟𝑠) is denumerable.
Showing the set of rational numbers is a denumerable set.
We must find bijective relation between ℕ 𝑎𝑛𝑑 ℚ
Consider the rational numbers arranged in the following array.
All numbers in nth column have numerator (𝑛+1)/2 if n is even and − 𝑛/2 if n is odd
All numbers in nth row have denominator n
Consider 𝑟𝜖ℚ, then 𝑟 = 𝑚/𝑛 : 𝑚𝜖ℤ, 𝑛𝜖ℕ
We can find r in the grid,
If m>0 then r is in (2m+1)th column and nth row
If m<0 then r is in (-2m)th column and nth row. If m=0, r=0, and it is included
So, every 𝑟𝜖ℚ is included in this grid.
Consider the arrowed sequence starting from 0. That sequence continues infinitely and we can order rational numbers using their position in the sequence.
Note that the same rational number can repeat, in that case, we consider only the first one.
Let 𝑓(𝑛: ℕ ⇒ ℚ) defines the nth rational number in the above-defined sequence. As the sequence is an ordered sequence for all 𝑛 ∈ ℕ there is an f(n)∈ ℚ
So, f(n) is a well-defined function.
Let r𝜖ℚ,
As stated earlier, r is included in the above series. So, r should have its position in the series. This means there exists 𝑛𝜖ℕ such that f(n)=r
For all r𝜖ℚ there exists 𝑛𝜖ℕ such that f(n)=r So Range(f)=Codomain(f)
Therefore f(n) is surjective.
Let 𝑥1 𝑎𝑛𝑑 𝑥2 be two elements in ℕ
Suppose 𝑓(𝑥1) = 𝑓(𝑥2)=r
When we defined the sequence, we defined that if r is repeated in the sequence only the first time it will be added to the sequence and the rest will be eliminated.
As r can only appear in the sequence once, 𝑥1 = 𝑥2
𝑓(𝑥1) = 𝑓(𝑥2) ⇒ 𝑥1 = 𝑥2
Therefore 𝑓 is injective
As f is injective and surjective f is bijective.
So there exists a bijective relation between ℕ 𝑎𝑛𝑑 ℚ
So ℚ is denumerable.
Real numbers in (0,1) is not a denumerable set
Suppose (0,1) is denumerable. There should be a function f(n),
𝑓(𝑛: ℕ ⇒ (0,1)) is bijective.
So, f(n) should be surjective.
For every 𝑎 ∈ ℚ there should be 𝑛𝜖ℕ such that f(n)=a
And any a in (0,1) can be expressed in the number line, So can be written as a number with n decimal places.
So, we can write it as, f(1) = 0.xxxxxxxxxxx f(2) = 0.xxxxxxxx
f(3)= 0.xxxxxxxxxxx
…
…
…
f(n) = 0.a1 a2 a3 a4 a5 a6 a7…….. an………….
we will now define a new number b in (0,1) as follows
Let bn be the nth decimal point of b
We choose bn such that it is neither of 0,9 or nth decimal point of f(n)
For an example
if f(1)=0.67868 then we have to choose b1 such that b1 ≠ 0,9 or 6
if f(8)=0.9834688369 then we have to choose b8 such that b8 ≠ 0,9 or 8
Now consider b.
If for any n in natural numbers f(n)=b, then their decimal representations should be similar. Which implies bn = nth decimal point of f(n)
But we choose such that bn ≠ nth decimal point of f(n)
Therefore b ≠ f(n) for any 𝑛𝜖ℕ
But b has a decimal representation. So can be expressed in the number line. So b is a real number.
And any decimal point of b is neither 0 nor 9.
So b ≠ 0.0000000000000000….. or 0.9999999999999999999999….
So b lies strictly between (0,1)
This implies there exists b∈ (0,1) such that there is no 𝑛 ∈ ℕ f(n)=b
So f can’t be surjective.
This is a contradiction.
So (0,1) is not denumerable.
Cardinality of a set
As mentioned in the history and flow, once got to know that every infinite set is not the same size, it made people think about a new parameter as the measure of the size of an infinite set.
In the beginning, the size of an infinite set was referred to by many terms but modern mathematicians use the word cardinally to describe the size of the infinite set.
As mentioned in the introduction, the idea of the size of an infinite set was brought by Cantor. He defined the size of a set as
Two sets M and N are equivalent . . . if it is possible to put them, by some law, in such a relation to one another that to every element of each one of
them corresponds to one and only one element of the other.
So modern mathematicians refer to this size as cardinality.
So, two sets are having ‘same cardinality’ if those 2 sets are equivalent as in Cantor’s equivalence definition above.
Even though this definition was first introduced for finite sets, this same definition can be extended for infinite sets as mentioned in the introduction.
This was a huge breakthrough as during that time infinite was identified only as potential infinity.
But with this, infinite can also be identified as completed infinite.
If A is a set ‘Cardinality of set A’ is denoted by 𝐴̅
Denumerability is also a special case of cardinality. Denumerability is having the same cardinality as Natural numbers.
Set of real numbers and real numbers in (0,1) have the same cardinality
To show that ℝ and (0,1) have the same cardinality we should show that there exists a bijective function between ℝ and (0,1).
Let 𝑓(𝑥: (0,1) ⇒ ℝ) = tan[π(x + 1/2)]
Let f(x)=t; t∈ ℝ
t= tan[π(x + 1/2)]
x = 1/𝜋 𝑡𝑎𝑛−1𝑡 − 1/2
for all t∈ ℝ;
− 𝜋/2 < 𝑡𝑎𝑛−1𝑡 < 𝜋/2
0 < 1/𝜋 𝑡𝑎𝑛−1𝑡 − 1/2 < 1
0 < 𝑥 < 1
Therefore, for any t∈ ℝ, there exists a x∈ (0,1) such that f(x)=t Range(f)= ℝ = Codomain(f)
Therefore 𝑓((0,1) ⇒ ℝ) is surjective.
Let 𝑥1 𝑎𝑛𝑑 𝑥2 be two elements in (0,1)
Suppose 𝑓(𝑥1) = 𝑓(𝑥2) = 𝑡 ; 𝑡 ∈ ℝ
t= tan[π(𝑥1 + 1/2)] = tan[π(𝑥2 + 1/2)]
0= tan[π(𝑥1 + 1/2)] – tan[π(𝑥 + 1/2)]
0 = tan[π(𝑥1 + 1/2) – [π(𝑥2 + 1/2)] / 1+tan[π(𝑥1 + 1/2)] * tan[π(𝑥2 + 1/2)]
0 = tan[π(𝑥1 − 𝑥2)]
π(𝑥1 − 𝑥2) = nπ
(𝑥1 − 𝑥2) = n n=….,-1,0,1,…..
𝐵𝑢𝑡 𝑏𝑜𝑡ℎ 𝑥1 𝑎𝑛𝑑 𝑥2 are two elements in (0,1)
Wlog, let 𝑥1 > 𝑥2
As 𝑥1, 𝑥2 ∈ (0,1)
0≤ 𝑥1 − 𝑥2 < 1
So n can be only 0.
Therefore 𝑥1 = 𝑥2
𝑓(𝑥1) = 𝑓(𝑥2) 𝑖𝑚𝑝𝑙𝑖𝑒𝑠 𝑥1 = 𝑥2
𝑓((0,1) ⇒ ℝ) is injective.
So there exists a bijective function between (0,1) and ℝ
So cardinality of Real numbers is equal to the cardinality of real numbers in (0,1).
Featured Image: https://bit.ly/3ZGuaui
Content Image 1: https://bit.ly/3ZGuaui
Content Image 2: https://bit.ly/3ZkGjWa