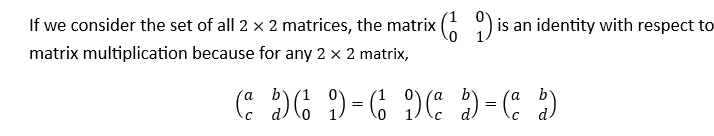When we see “+” and “x” in a mathematical expression, we immediately do that operation without a second thought about what makes such an action possible. We even have extended the concept of “adding” beyond numbers to apply to matrices and vectors. However, there must be some fundamental properties of these operations and these quantities that we operate on that make them seemingly related.

Algebraic structures

An algebraic structure is a nonempty set together with a collection of operations governed by a list of axioms (An axiom is a basic statement assumed to be true on which other results are derived). A key point to note is that the elements of those sets and the manipulations we do to them don’t necessarily have any meaning, hence the use of the term “abstract” here. The properties of these algebraic structures and relationships among them are what abstract algebra concerns with.

Groups, rings and fields are some of the commonly studied algebraic structures, all of which are sets in essence. As for their elements?  They can be almost whatever you want, be it numbers, vectors, matrices, arrangements of letters or even the many ways to rotate a Rubik’s cube!

Some basic definitions

Binary Operations

A binary operation is a rule for manipulating two elements from the same nonempty set, which results in another element of that same set. The concept of the binary operation underpins every subsequent definition thereafter, so we shall see some examples.

The addition of real numbers that we know well, ƒ(a,b)= a+b, is a binary operation since the sum of two real numbers is also a real number. In usual notation, it is denoted by the expression +: R x R → R

The matrix addition of 2×2 matrices is also a binary operation since the sum of two 2×2 matrices is also a 2×2 matrix.

Let G be a nonempty set and let ∗ be a binary operation on G. Take elements a, b and c from G. Note that we haven’t defined exactly what * and G are, so they can be any operation and set. In the standard notation it is written as *: G x G → G. The operation a*b is read out as “a-star-b”.

 

Associativity

(a * b) * c = a * (b * c) For all a, b and c in G

In the usual procedure of evaluation, we know that (1 + 2) + 3 = 1 + (2 + 3) = 6. Not only that, but we also know it’s true for any real number. This result is possible because of the associative property of addition of real numbers.

However, in the case of the division of nonzero real numbers;

(1 ÷ 2) ÷ 3 = 1/2 ÷ 3 = 1/6

1 ÷ (2 ÷ 3) = 1 ÷ 2/3 = 3/2

Since (1 ÷ 2) ÷ 3 ≠ 1 ÷ (2 ÷ 3) , we conclude that the division of nonzero real numbers is not associative.

 

Identity

It is an element e in G  such that  a * e = e * a  = a for all a in G. 

Consider the addition of real numbers, here it will be our choice for the  operation. Then the number 0 is an identity with respect to  because for any real number a,

a + 0 = 0 + a = a

 

 

Inverses

Given a in G, the inverse of a is some b in G such that a * b = b * a = e  ( e is the identity)

Consider the addition of real numbers as before. Since real numbers (R) include both positive and negative numbers, for each a in R there will be some (-a) in R such that a + (-a) = 0, which is the aforementioned identity for + in R. Hence -a is the inverse for any a in R.

 

Groups

 

 

Groups are a very commonly studied and used algebraic structure. Let us see what it precisely is and some examples for it.

Let G be a nonempty set and let * be a binary operation on G. A group is a set G, together with a binary operation ∗ that holds the properties:

1. Associativity
2. Existence of identity
3. Existence of inverses

(Z, +) is a group. This represents the addition of integers (Z is the integer set). While we intuitively know that associativity holds for this operation, that the identity is 0 and that inverses exist, we can take some arbitrary elements and prove that all 3 properties hold. In fact, that’s how we obtain similar results for every group we consider.

Consider the binary operation  * R \ {1}: x R \ {1} → R{1} given by a * b = a + b  a.b ( R \ {1} are all the numbers in R without 1, we shall see why 1 doesn’t work here). Note that + and – denote the usual addition and subtraction, and a.b denotes the usual multiplication of a and b.

(R \ {1}, *) forms a group. Here the identity e=0 because a * 0 = a + 0 – a.0 = a

Now for the inverse, for a*b = e = 0 , it must be that a + b -ab = 0.

This gives that b = -a/ (1-a), which is defined only for a ≠ 1 otherwise we get division by zero which is undefined.

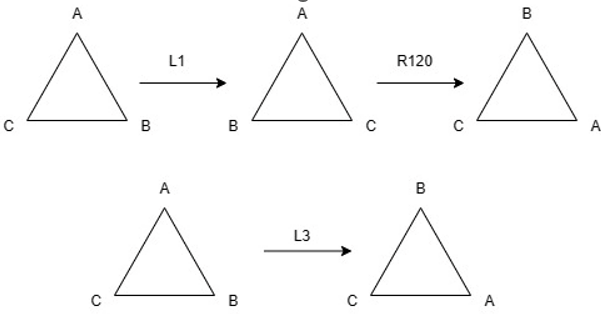
In a different vein, let us consider the symmetries of a regular triangle. These form a set where the elements are not numbers but different ways to rotate and reflect a triangle. For example, R₁₂₀ means to rotate the triangle by 120° clockwise. L₁ is a reflection around the perpendicular bisector of CB. These rotations and reflections form what is called the Dihedral group D_3.

Composition of functions is a binary operation a ° b where a and b are rotations or reflections. What it means is to take the triangle at any orientation and apply the reflection or rotation and then apply the “a” reflection or rotation to the previous result. An example would be R_{120 °} L₁ = L₃ which is to say that applying L₁ (reflection around the perpendicular bisector of CB) and then R₁₂₀ is equivalent to applying L₃ once (reflection around the perpendicular bisector of AB).

It can be proven that the set D₃ forms a group under composition of functions. Under this operation you have R₀ (Rotation by 0°) as the identity. With this example we see that groups don’t necessarily have to be sets of numbers, and that their binary operation doesn’t have to be the usual arithmetic operations but even geometric transformations. It is precisely the abstract nature of the concept of “group” which allows for this variety, which is vaster than this article attempts to convey!

Abstract algebra in the wild

The notion of “symmetry” is central to many mathematical representations of phenomena in physics (especially particle physics), and groups are used to describe them. Those symmetries give rise to the many conservation laws of systems. In chemistry and materials science, crystal structures are classified using what are called “space groups”. They are symmetrical groups of an object in space, akin to the symmetries of the triangle we discussed above.

Furthermore, abstract algebra is essential in other aspects of mathematics, especially for obtaining results in specific problems. Rings, which are groups with some extra conditions, are used in algebraic number theory to study properties of integers. The fact that there is no formula for the roots of a quintic equation (ax⁵ + bx⁴ + cx³ + dx² + ex + f = 0 ) was proved using Galois Theory, another branch of abstract algebra.

 

References links:

1. Towers, M. (2020, May 11). 4.2 Examples of groups | MATH0007: Algebra for Joint Honours Students. https://www.ucl.ac.uk/~ucahmto/0007/_book/4-2-examples-of-groups.html
2. Alexander Paulin. (n.d.). https://math.berkeley.edu/~apaulin/
3. Abstract Algebra | Brilliant Math & Science Wiki. (n.d.). https://brilliant.org/wiki/abstract-algebra/

Image Courtesy:

1. Featured image: https://bit.ly/3BVcEJ8
2. Image 1: https://bit.ly/3WDtF3X
3. Image 2: https://bit.ly/42cheNA
4. Image 3: https://bit.ly/43qudMM

Tagged : Abstract algebra / algebra / mathematics