“Mathematics is the language with which God has written the universe.”

∼Galileo Galilei

According to the all-mighty knowledge base, Wikipedia, mathematics is an area of knowledge that includes the topics of numbers, formulas, related structures, shapes, and the spaces in which they are contained, and quantities and their changes. This so-called language of the universe includes some major subdisciplines such as Number theory, Calculus, Analysis, Algebra, and Geometry. This subject is a really interesting subject that helps us to understand and work with numbers, shapes, patterns, and logical reasoning. Simple mathematics is all about counting, measuring, and describing things in a more organized and precise way. It helps us to get some proper answers to questions like, “How much?”, “How many” and find the patterns and links between various parameters that the whole world depends on.

For example, if you want to know how much money you’ll have after saving a certain amount each month, mathematics can help you calculate it. If you want to figure out the area of a rectangular room, mathematics can help you find the right formula to get the answer. It also plays a crucial role in everyday activities like telling time, measuring ingredients for a recipe, or budgeting your salary. And mathematics is not only about numbers and symbols which construct mind-bending equations and theories like in algebra but also about understanding and describing shapes and their properties.

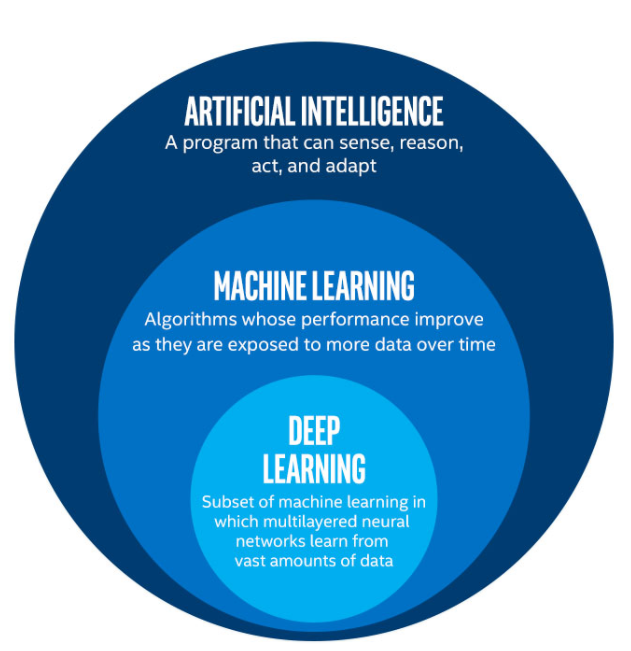
And our supporting roles here, AI and ML. What are they? Why is this 21^st century so serious about these few letters? Artificial Intelligence or AI is a field of study in Computer science that focuses on creating intelligent machines that can think and respond like humans. It’s about designing and developing computer programs and systems that can understand, reason, and make decisions on their own, without being explicitly programmed for every task.

Just like our brains learn from experience, AI systems can learn from data. They use special algorithms and techniques to analyze large amounts of information and recognize patterns. This allows them to perform tasks like recognizing texts and images, understanding speech, generating content, and even playing complex games such as Go and Chess. AI also has a vast amount of practical usage such as generating creative content, translating languages, giving out better recommendations, and assisting on find human diseases as well.  AI systems can adapt and improve over time, getting better at their tasks as they gather more information. So, there is no doubt that AI is changing the way people do their everyday tasks.

Machine Learning or ML is a major subdiscipline of AI that focuses on teaching machines to learn from experience and get better over time, just like humans do.  That is more accurate to describe this as training a computer or a machine to learn by itself, recognize patterns and respond accordingly to them. In traditional computer systems and programs, humans should tell them everything that has to be done. But in AI and ML, human only needs to give some amount of data and let them figure out the existing patterns and makes their own decisions.

Here’s how it works: First, we provide the computer with a lot of examples or data. The computer analyzes this data and looks for patterns and relationships. It tries to learn from these patterns so that it can make predictions or decisions on new, unseen data. The more examples the computer sees, the better it becomes at recognizing patterns and making accurate predictions. It keeps learning and improving as it gets more data. Machine Learning is used in various applications, like voice recognition, recommendation systems, and even self-driving cars. It’s an exciting field that helps computers become smarter and more helpful in our daily lives.

Given our understanding of mathematics, AI, and ML, we come to an important question: how do these elements interconnect? While it’s clear that AI and ML are closely related, the role of mathematics in this collaboration becomes essential to explore. Mathematics, renowned for its proficiency in handling numbers, shapes, and patterns, plays a significant role in the realm of AI and ML. So, how exactly do numbers, shapes, and patterns intertwine with AI and ML, and what significance do they hold in these fields?

Mathematics forms the fundamental basis that holds profound significance within the fields of Artificial Intelligence and Machine Learning. It serves as the bedrock, providing a solid foundation for understanding, developing, and advancing intelligent systems. By harnessing the power of mathematical principles, researchers and practitioners gain invaluable tools and techniques to generate complex patterns, construct robust algorithms, and enable machines to learn, adapt, and make informed decisions. The interconnection between mathematics and AI/ML lays the groundwork for groundbreaking advancements in the realm of intelligent technologies.

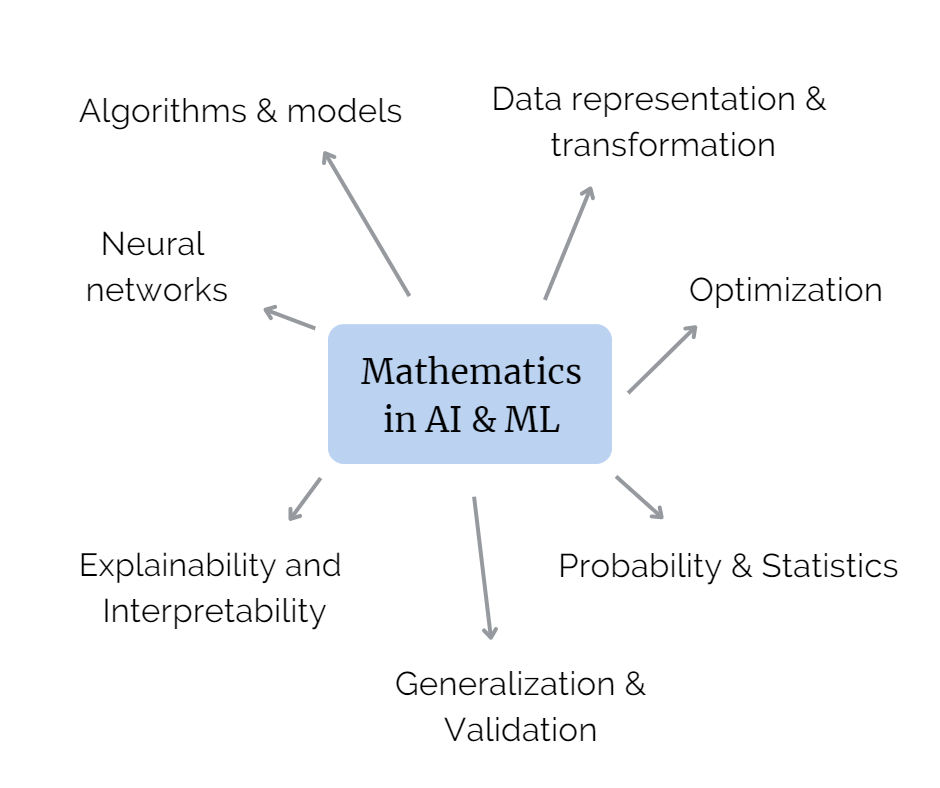
Here are some examples of use cases of mathematics in the fields of AI and ML, shaping their methodologies and advancements.

• Algorithms and models

Mathematics plays an important role in the design and analysis of algorithms and models utilized in AI and ML, employing concepts from linear algebra, calculus, probability theory, and statistics. These mathematical foundations enable the development of algorithms capable of processing and analyzing vast volumes of data, making accurate predictions, and acquiring knowledge from experience.

• Data representation and transformation

Mathematics serves as a powerful tool for representing and transforming data in a meaningful manner, facilitating efficient manipulation, analysis, and visualization of complex data sets. Techniques such as matrix operations, vector spaces, and dimensionality reduction play a vital role in enabling AI and ML algorithms to extract pertinent features and patterns from the data. By leveraging these mathematical methods, AI and ML systems can uncover valuable insights and make informed decisions based on complex datasets, ultimately enhancing their overall performance and capabilities.

• Optimization

Optimization problems are inherent to AI and ML algorithms, as they aim to find the optimal solution or parameter set that minimizes or maximizes a given objective function. Mathematical optimization techniques, including gradient descent, convex optimization, and numerical methods, are extensively employed to tackle these problems and refine models for optimal performance. By leveraging these mathematical tools, AI and ML practitioners can effectively navigate complex search spaces, iteratively adjust model parameters, and converge toward the best possible solution, enhancing the overall efficiency and effectiveness of the algorithms.

• Probability and statistics

Probability theory and statistics play a vital role in AI and ML by providing the necessary tools to handle uncertainty and make probabilistic inferences. Fundamental concepts such as Bayes’ theorem, hypothesis testing, and statistical distributions are pivotal in modelling uncertainty, estimating probabilities, and enabling informed decision-making based on data. These mathematical foundations empower AI and ML practitioners to quantify uncertainty, assess the reliability of predictions, and optimize models for robust performance. By leveraging probability theory and statistical analysis, AI and ML systems can effectively navigate uncertain scenarios, enhance the reliability of their predictions, and enable data-driven decision-making in real-world applications.

• Neural networks

Neural networks serve as a foundational component in contemporary AI and ML, with their mathematical based backbone relying on linear algebra, calculus, and optimization. Mathematical principles come into play through concepts such as backpropagation, activation functions, and gradient descent, enabling the training of neural networks and enhancing their accuracy. By leveraging these mathematical foundations, neural networks can efficiently process and learn from complex data, iteratively adjust their parameters, and optimize their performance. The mathematical framework behind neural networks provides the means to model and solve intricate problems, unlocking their potential for tasks such as image recognition, natural language processing, and predictive analytics in AI and ML applications.

• Generalization and validation

Concepts like cross-validation, loss functions, and evaluation metrics such as precision, recall, and F1 score are employed to assess the models’ generalization capability and robustness. These mathematical techniques enable informed decision-making in selecting the most effective algorithms and architectures for a given task. By quantitatively evaluating the performance of AI and ML models, researchers can gain insights into their strengths, weaknesses, and areas of improvement, fostering the development of more accurate and reliable intelligent systems.

• Explainability and Interpretability

The mathematical foundations of AI and ML also contribute to the interpretability and explainability of models. Techniques such as feature importance analysis, dimensionality reduction, and visualization methods allow researchers to understand and interpret the decision-making process of complex models, making them more transparent and trustworthy.

For all those use cases like optimization, neural networks, generalization, etc mathematics has a special role of providing a strong backbone. But what topics of mathematics are involved in those use cases providing that strong backbone needed for the methodologies and advancements of AI and ML? Here are some examples of topics that are heavily involved in the AI and ML fields.

• Linear Algebra

Linear algebra plays a crucial role in AI and ML due to its importance and wide range of applications. It provides a powerful framework for representing and manipulating data in the form of vectors and matrices. Linear algebra enables efficient computations involved in various AI and ML tasks, such as data preprocessing, dimensionality reduction, feature extraction, and model optimization. Techniques like matrix operations, eigenvalue decomposition, and singular value decomposition are extensively utilized in tasks like image recognition, natural language processing, recommendation systems, and deep learning. Moreover, linear algebra provides the foundation for understanding and implementing popular algorithms, including linear regression, support vector machines, and neural networks. Its versatility and effectiveness in handling large-scale data and complex mathematical operations make linear algebra a necessary tool in AI and ML research and development.

• Vectors and vector analysis

Vectors hold significant importance and find numerous applications in the fields of AI and ML. They serve as fundamental entities for representing and organizing data in a concise and structured manner. Vectors play a crucial role in capturing features and characteristics of data points, enabling efficient calculations and comparisons. In AI and ML, vectors are employed for tasks such as text analysis, image recognition, sentiment analysis, and recommendation systems. They facilitate operations like similarity measurements, clustering, and classification, aiding in the extraction of meaningful patterns and relationships from data. By utilizing vectors, AI and ML algorithms can effectively process, analyze, and model complex datasets, leading to enhanced decision-making, prediction accuracy, and overall system performance.

• Matrix theory

Matrices provide a versatile framework for organizing and manipulating structured data. They are extensively employed for tasks such as data preprocessing, feature extraction, and model optimization. Matrix operations, including multiplication, inversion, and eigenvalue decomposition, play a pivotal role in linear transformations, dimensionality reduction techniques like Principal Component Analysis (PCA), and regularization methods such as Ridge and Lasso regression. Matrices also serve as a foundation for various AI and ML algorithms, including linear regression, support vector machines, and deep learning neural networks.

• Eigenvalues and eigenvectors

They provide crucial insights into the behavior and characteristics of linear transformations and matrices. In AI and ML, eigenvalues and eigenvectors are utilized for dimensionality reduction, feature extraction, and data representation. Techniques like Principal Component Analysis (PCA) leverage eigendecomposition to identify the most informative and representative features in high-dimensional datasets. Eigenvectors also play a vital role in graph analysis and clustering algorithms. Furthermore, eigenvalues are used to assess the stability and convergence properties of iterative algorithms, such as power iteration in eigenvector computations. With a better understanding of eigenvalues and eigenvectors, AI and ML practitioners can help to extract meaningful features and gain deeper insights into the structure and properties of data, leading to improved performance and efficiency in various tasks.

• Calculus

Calculus provides a powerful mathematical framework for analyzing and modelling dynamic processes, optimizing functions, and understanding the behavior of complex systems. In AI and ML, calculus is instrumental in various areas. Differential calculus enables the computation of gradients and derivatives, which are essential for optimizing model parameters using techniques like gradient descent. Integral calculus plays a crucial role in probability density estimation, calculating areas under curves, and solving optimization problems. Calculus also aids in analyzing the convergence and stability of iterative algorithms used in training neural networks.

To have a better insight into the fields such as machine learning and artificial intelligence a strong proficiency in mathematics is essential. Mathematics plays a pivotal role in these fields, enhancing analytical thinking skills that are fundamental to artificial intelligence. While some may perceive AI as a mystical phenomenon, it is not magic but the power of mathematics that underlies all its advancements. Mathematics is the driving force behind the remarkable inventions and breakthroughs in AI. To excel and make a significant impact in today’s AI-driven world, a solid foundation in mathematics is essential, as it equips individuals with the necessary tools to comprehend and innovate within the realm of artificial intelligence.

Image Courtesies:

Featured Image: http://bitly.ws/QaJv

Image 1: http://bitly.ws/QaJJ
Image 2: http://bitly.ws/QaJS
Image 3: http://bitly.ws/QaK8
Image 4: http://bitly.ws/QaKd
Image 5: http://bitly.ws/QaKh