This time I’m going to prove a geometric dilemma. Just like my 1st proof for the equality between 1 and 2 the result I get is totally absurd. So , here we go……
Theorem: All the triangles are equilateral.
Proof: Let ABC be a general triangle
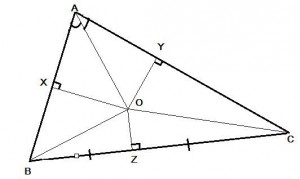
As indicated in the diagram above, we have constructed some lines such that O is the intersection point of the angle bisector of Â(namely AO) and the perpendicular bisector of BC (namely OZ). X and Y are the feet of the altitudes from O to AB and AC respectively. Z is the midpoint of BC.
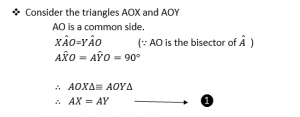
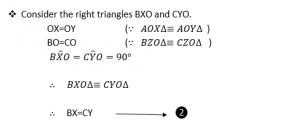
From ❶+❷ we get ,
AX+XB=AY+YC
AB=AC
Similarly we can prove that , AC=BC
∴ AB=BC=CA
This means, whatever the triangle ABC is , it is equilateral !!!!.
(For an example if you take a triangle with side lengths 1,2 and 2 then above proof implies that 1=2=2, simply 1=2 😉 )
So , without going any further I leave the challenge of resolving this dilemma to you guys…… 🙂