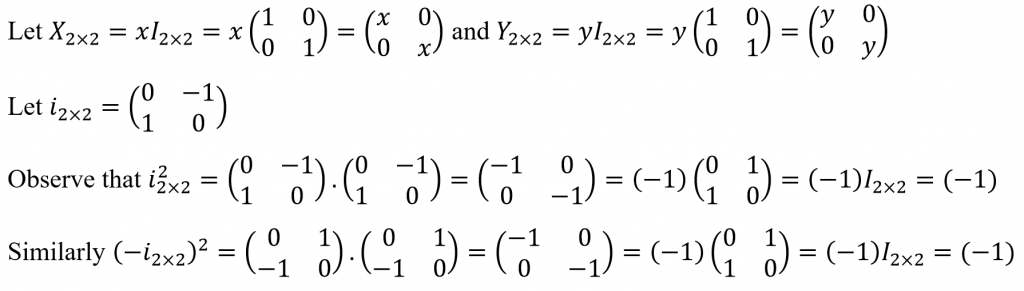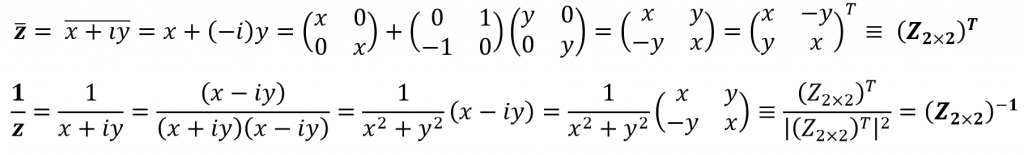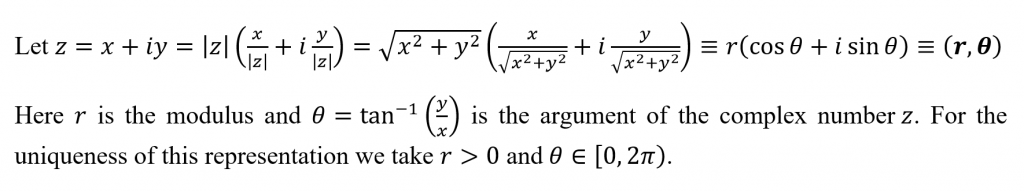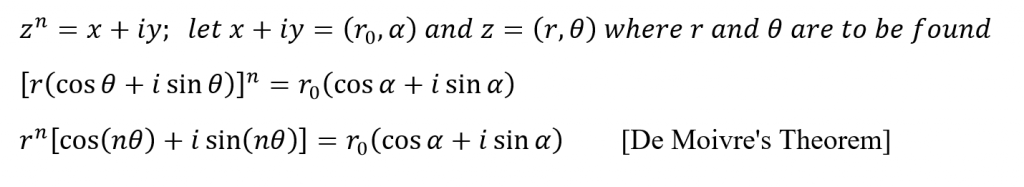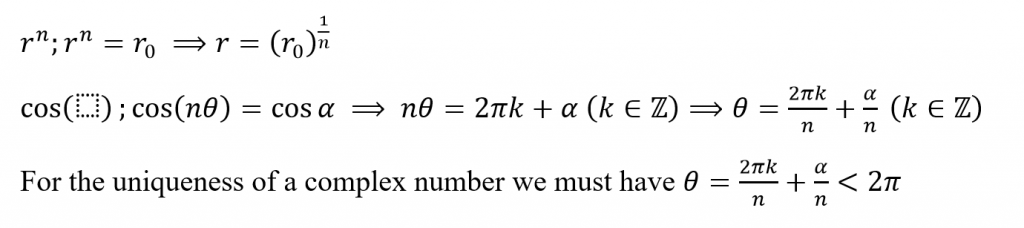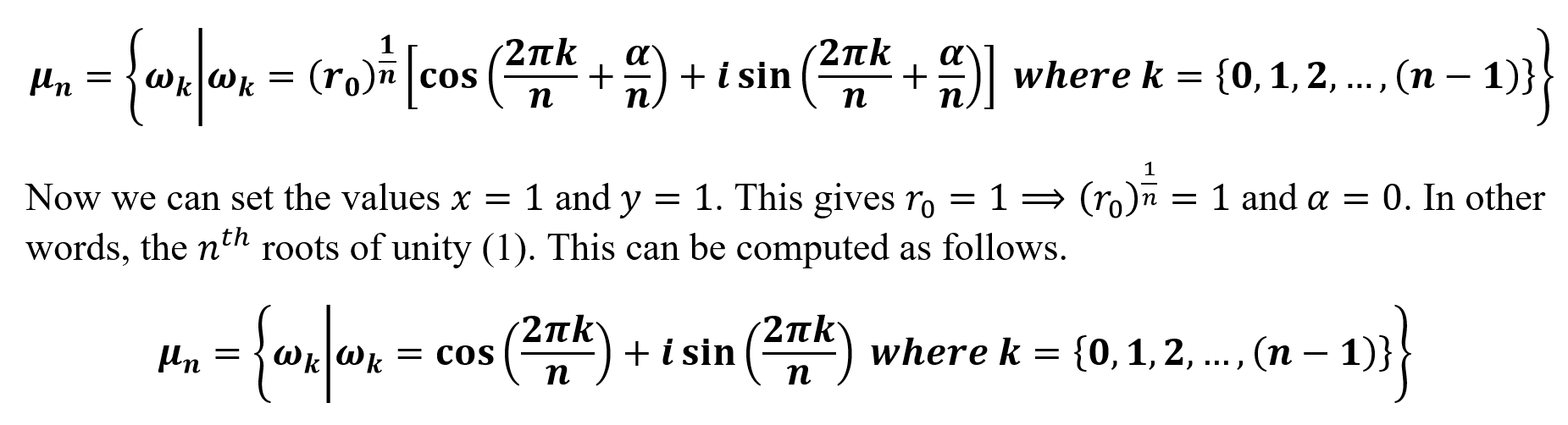In our progression in understanding the foundations of abstract algebra, we came across complex polynomials and their factors. From this, we finally arrived at imposing the question of finding the n^th roots of unity. Let’s start out with some basic theorems regarding complex numbers first.

Representation of Complex Numbers

Let’s consider a complex number z = x + iy where x and y are real scalars and i is a function projecting a real expression on to the complex plane. We can use a matrix representation for this as follows.

Now observe the following simplification.

This representation can be easily used to verify mathematical operation on complex numbers as well as derive expressions for the following.

We can also represent complex numbers using polar coordinates as in below.

De Moivre’s Theorem

De Moivre’s theorem describes the integer powers of a complex number. By the Principle of Mathematical Induction, we can prove this theorem as follows.

n^th Roots of a Complex Number

Consider a complex number z = x + iy now. Using the polar coordinate representation for x + iy and parametrically representing z, we obtain the following.

Now we can simply do a comparison and obtain the necessary parameters.

Thus we have obtained the expressions for the parameters set out. For each non-negative integer value of k we will obtain a root of the complex number. If we represent w_k as the k^th root of the set of n^th roots of the complex number, we can write this using set notation as follows.

Representing the n^th Roots of Unity

From this, it is easy to see that the set of n^th roots of unity can be generated by using elements. This step provides us with a visual image of how the n^th roots are situated in the Argand plane.

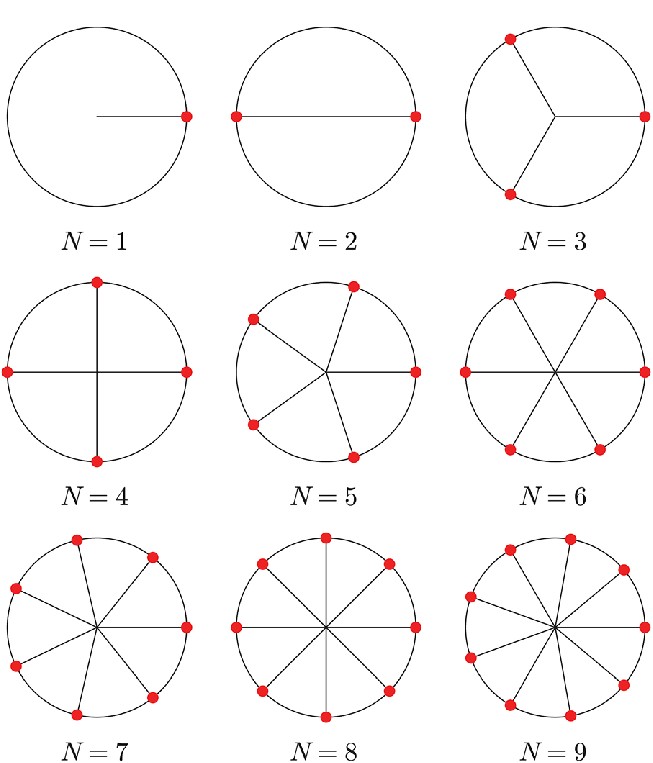
Since we know that the modulus of all the roots are the same (= 1), we can summarize this as simply points on the circumference of a circle with radius 1 placed at an angular difference of  2*pi/n to each other.

The diagram above shows the placement of these points corresponding to the table above. It is of importance to note that if we joined adjacent points then we get a regular n-gon.

By observing the diagram we can see that in certain figures of n^th roots, other figures of n^th roots can be roughly seen held within them. For example, we can clearly see the triangle formed by the 3^rd roots of unity, and the hexagon formed by the 6^th roots of unity within the nonagon formed by the 9^th roots of unity.

Furthermore, each of these figures has a feature of symmetricity between them. This is due to the Conjugate Pairs Theorem outlined earlier, which says that for a root of a complex polynomial, the conjugate of that root is also a root.

Inferences

By observing the graphical representations of the n^th roots of unity we can see the existence of a symmetricity. While the Conjugate Pairs Theorem plays an important role here, we can also consider the set generating element to play a vital role here as well. Finally, the containment of sets of lower-order roots in a  set of higher-order roots is of interest. By combining all of these, we arrive at the next step to understanding abstract algebra, symmetricity, and Cayley-tables.

References

01. http://www.phschool.com/atschool/ap_misc/dwfk_precalc/pdfs/8e/Ch6_Section6.pdf

02. https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-i-first-order-differential-equations/complex-arithmetic-and-exponentials/MIT18_03SCF11_s6_9text.pdf

Image Courtesies

01.Featured Image: https://bit.ly/3gY6lYV

02.Image 1: https://bit.ly/3lqjFqQ