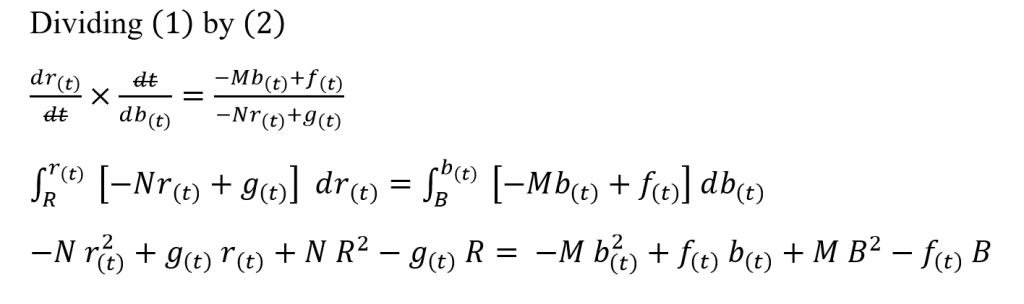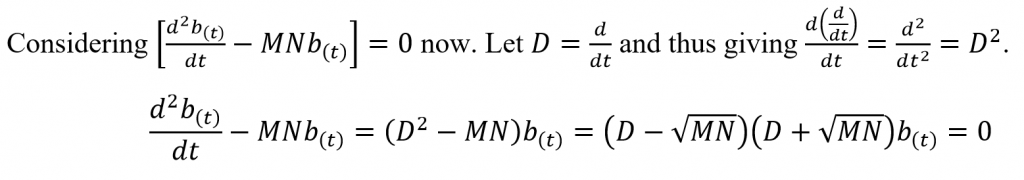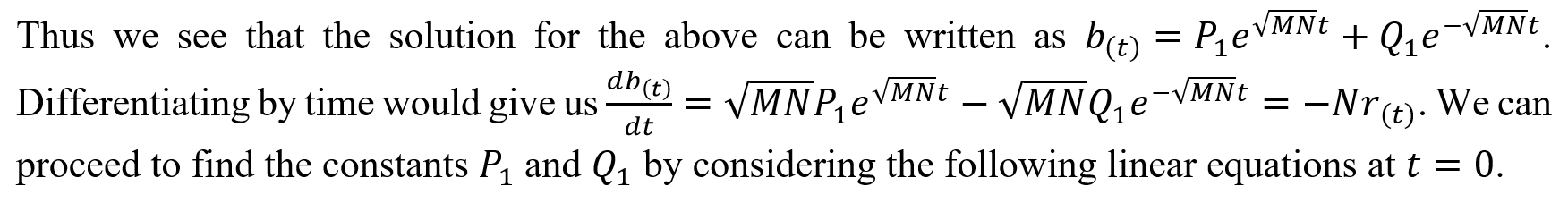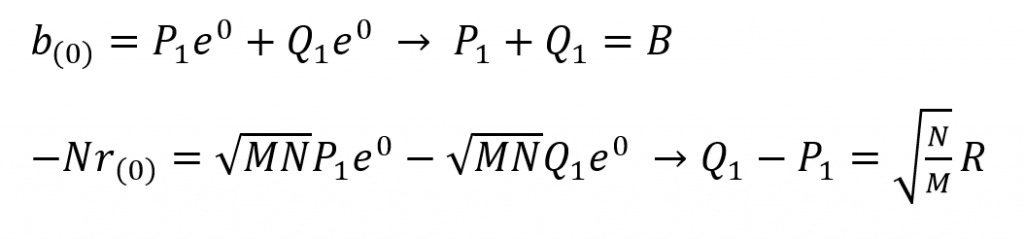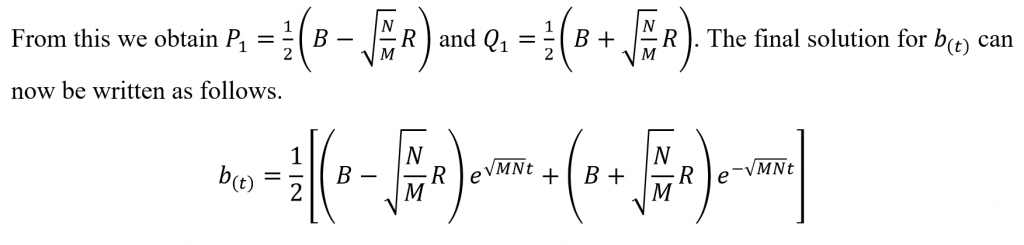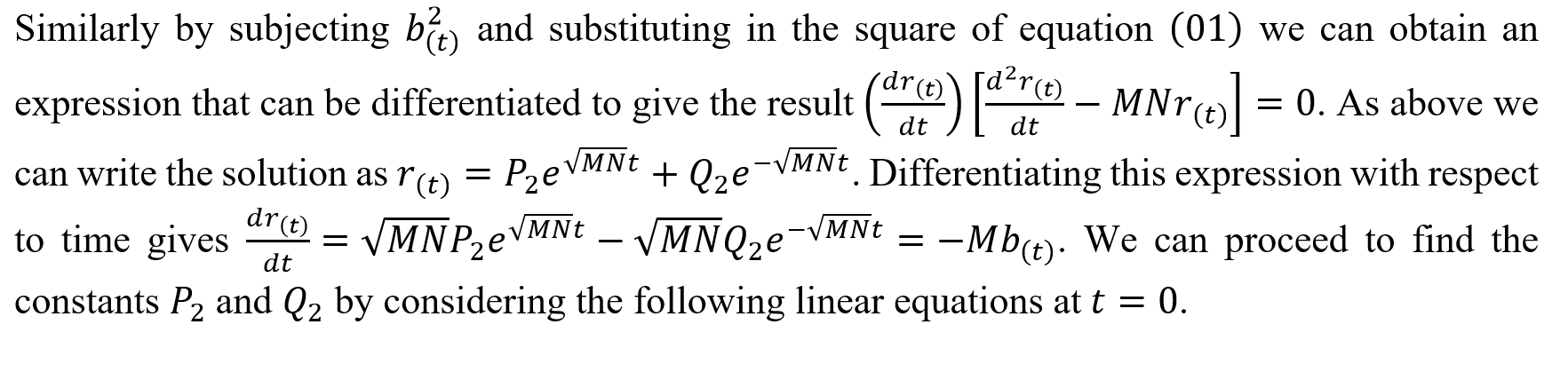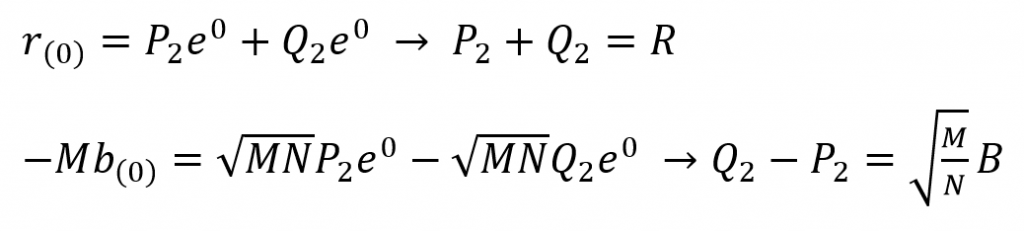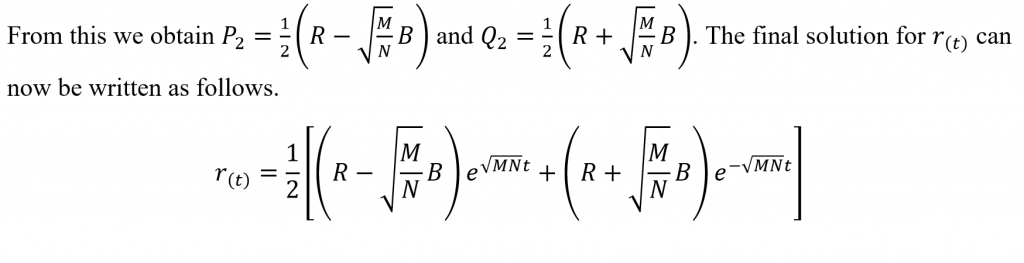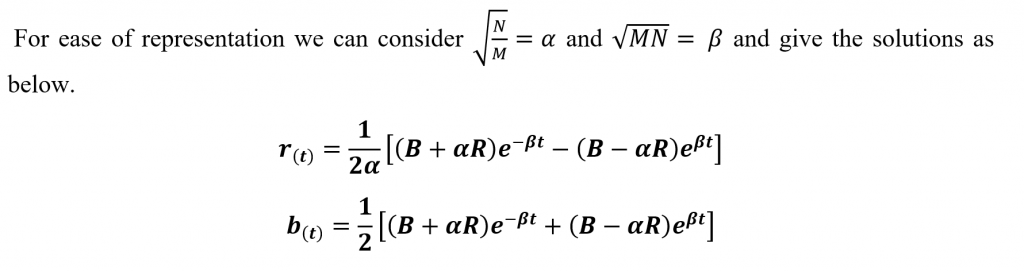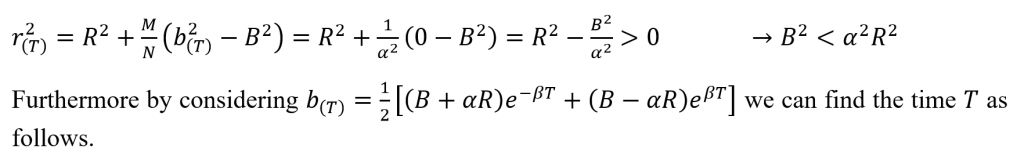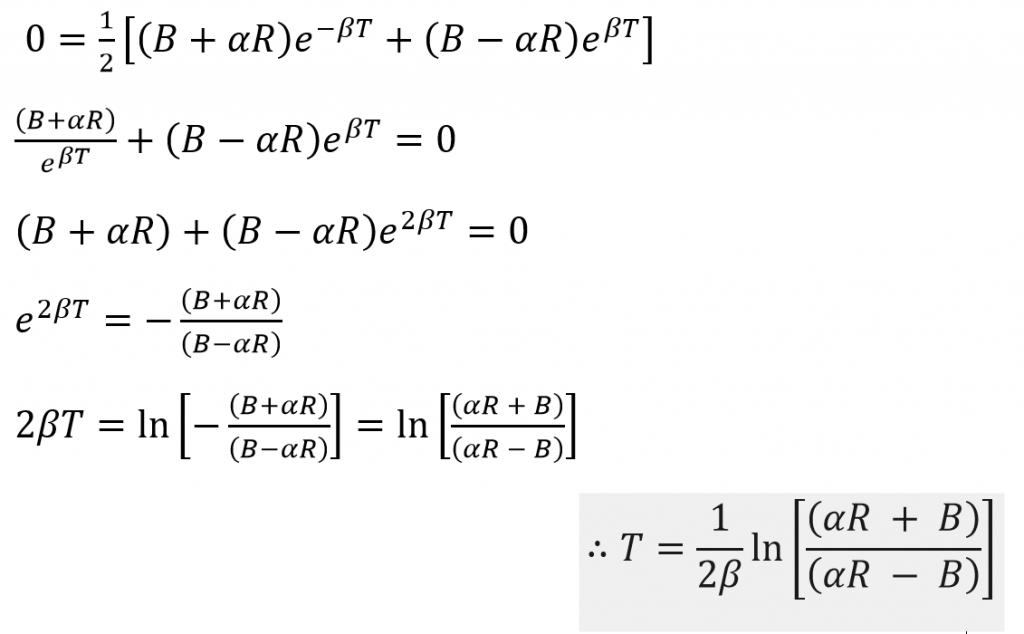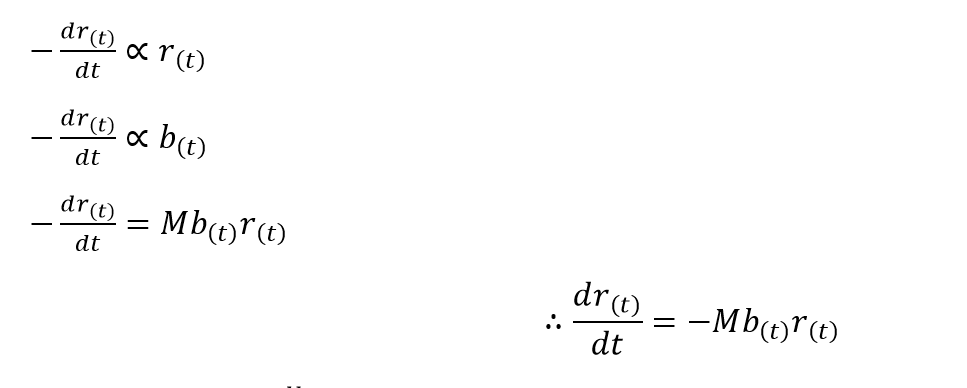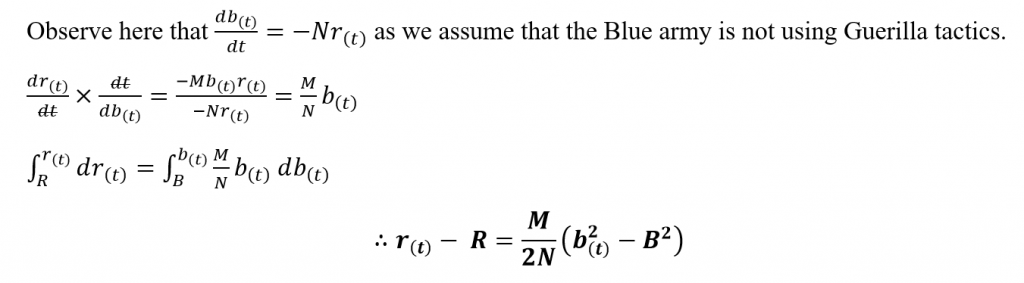We’ve seen how monkeys grew thumbs. Blessed with reason and free-will, we’ve watched them forge blades. Soon we saw monkey killing monkey over pieces of the ground. Step by step, the tools used were industrialized and mechanized. The English monk Roger Bacon’s description of the components of charcoal, sulfur, and saltpeter led to mixtures of the three being stocked in long tubes and propelled outwards through ignition. The 16th century saw the birth of the era-defining matchlock. The revolution of firearms that was brought about from it changed war forever.
While Lanchester’s Linear Law modeled ancient warfare, he proceeded to formulate a law fitting to modern warfare as well. As earlier, we will consider two opposing forces as follows. A Red army whose numbers at a given time is r(t) and a Blue army of numbers b(t) at the same instance. The initial numbers of each army are R and B respectively. Let the combat effectiveness coefficient of the two armies be N and M respectively.
Open Arena Warfare
First, we assume that the two armies are within the kill zone. The main difference from ancient warfare is the efficiency of concentrating forces. That is, as soon as one army suffers a loss, the opposing army’s forces concentrate on the remaining combatants of the first army. Therefore we can easily see that the rate of loss of strength of one army is proportional to the strength of the opposing army.
Another feature of interest in modern warfare is the quick response time to rally in reinforcements to the battlefield. The reinforcements would be a time-dependent value. Let the rate of obtaining reinforcements of the Red army be g(t) and that of the Blue army be f(t). We can easily conclude that the rate at which one army suffers losses is equal to the product of the strength of the opposing army and its combat effectiveness coefficient.
Solving the Equations
Before we analyze the above equations it is easier, to begin with, the analysis of the numbers of one army with respect to the other.
For ease of simplicity, let’s first consider the above equation with no reinforcements available to either army. That is g(t) = 0 and f(t) = 0.
Squaring (02) and substituting the above into it we obtain the following.
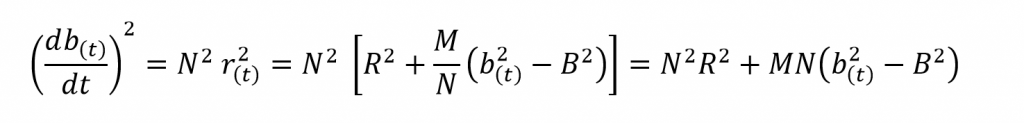Differentiating the above with respect to time now.
Analysis of Solutions
Consider that at a time t = T the battle ceases and the Red army is victorious. That is, the population of the Red army is greater than zero while that of the Blue army is zero.
Thus we can summarize the outcomes of the battles as follows.
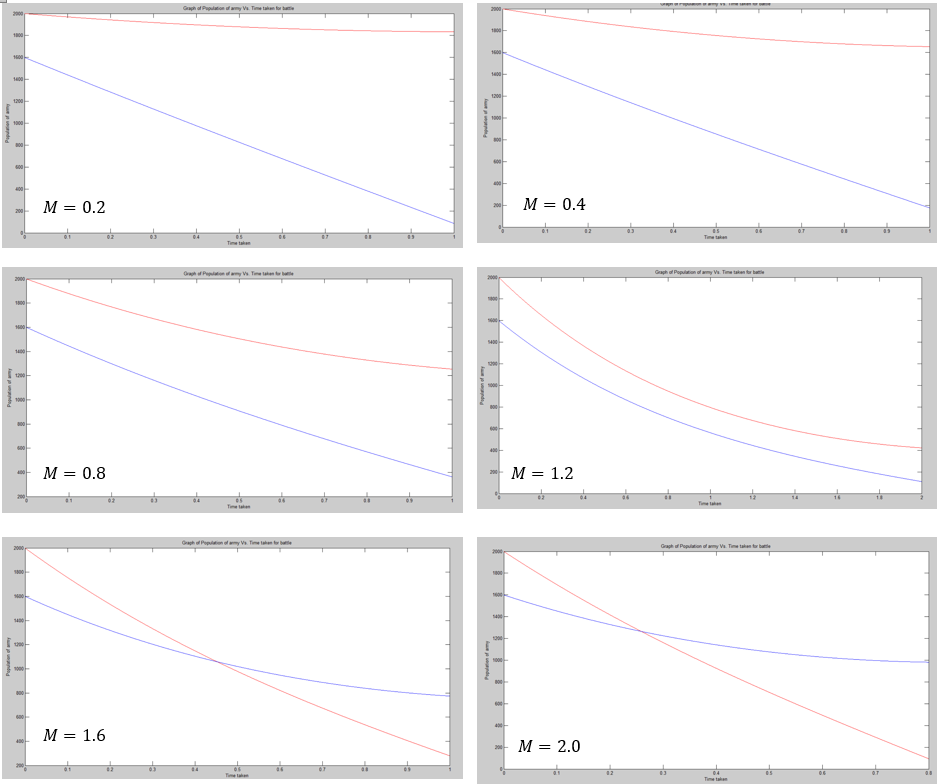
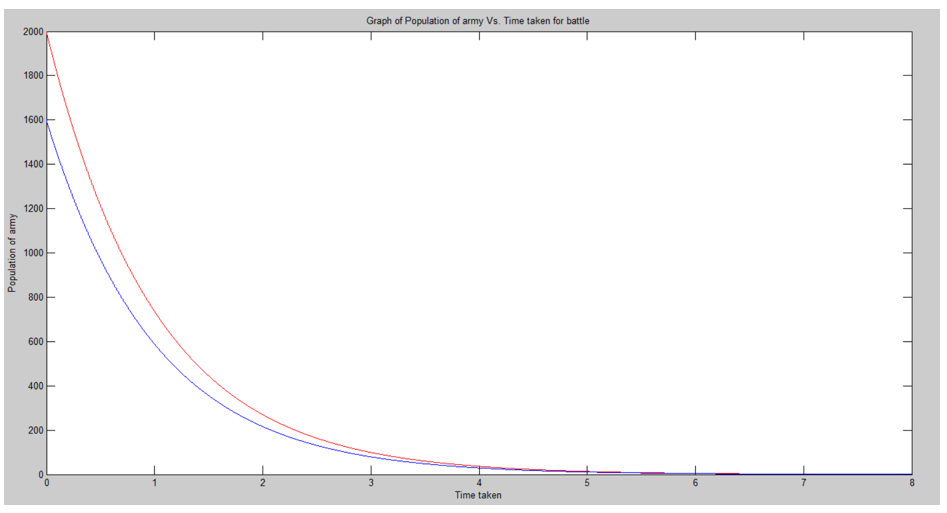
We can use MATLAB to examine the behavior of the solutions with the variation of parameters now. For example, consider R = 2000 and B = 1600. If we set the efficiency of the Red army (N) as 0.8 we can then observe the following.
An important graph here is that as the value of M approaches 1.25, which is when the outcome of the war would be a draw.
An immensely large time will be taken for the numbers of both armies to approach 0 as shown above.
Guerilla Warfare
As battle strategies developed, modern warfare was taken to a new height in the form of Guerilla warfare. Loosely describable as a small troop taking any form of cover available and battling successfully against a larger army. The phrase “any form of cover available” is of great importance as it shows clearly that the biggest disadvantage to troop employing Guerilla warfare is its numbers itself. The more the cover and the lesser the number in the Guerilla troop, the better the outcome. We can model this as follows.
Consider the Red army earlier, r(t) to be employing Guerilla tactics now.
A profound difference in the equation can now be seen. While the Red army populace is of the first order, a much larger second order of the Blue army populace is needed.
Tipping the Scales
The predictions given by Lanchester’s Square Law above are by assuming that only a single type of unit is battling another similar unit with the same resources. But in real war, that is not true.
Military strategy and science combined, brought out the need for roles in the battlefield. And to accompany those roles, modifications had to be done to the available firearms. The rather slow and short-range muskets that served the American Civil War were gradually replaced by gas-operated semi-automatic assault rifles. These were made into more compact and short-ranged heavy-hitting sub-machine guns.
Assault rifles and sub-machine guns became the standard choice of firearms in Guerilla warfare. The very high fire rate became important due to the very brief interval a Guerilla fighter would receive to fire back at the opposing force.
The pinnacle of engineering firearms was achieved with bolt action sniper rifles. The ability to take out a target over a very long range with extreme accuracy was granted. A knowledge of fluid dynamics and human anatomy, combined with extremely steady hands has led to the role of a sniper being revered and feared in any battlefield.
Send in Reinforcements!
Firearms, though effective greatly, were not to the desired effect. The limitations of flight path and effective area of impact of a bullet has led to the creation of more destructive weapons. The use of explosive devices in war balances this limitation. From the mobile grenade to the pressure-sensitive landmine, to Improvised Explosive Devices (IEDs) mankind has slowly developed means to cause bigger damage with lesser effort. This reached a peak on the 6th and 9th of August 1945 as the world watched billowing clouds rise over the cities of Hiroshima and Nagasaki.
Battlefields on the ground soon shifted to more intense battles on the seas and finally in the skies. Science and technology saw a new arena to develop in. From the sketches of submarines in Jules Verne’s literature to the multiple ton warhead carrying SSBN submarines science progressed. Science kept on progressing from the Wright’s first flight in Kittyhawk to the dog-fighting destruction of the McDonell Douglas F15E Strike Eagle.
As science and technology keep on progressing, budgets for militia keep increasing, and violence on the streets are becoming more widespread across the globe, it is a question to be asked whether “Progress for the sake of progress must be discouraged” after all.
Image Courtesies:
01. Featured Image: https://bit.ly/3hTTyqD
02. Image 1: https://cbsloc.al/39MkWUL
03. Image 2: https://bit.ly/3foZ6be
References:
01. Braun, M., 1993. Differential Equations and Their Applications. Fourth ed. New York: Springer Science+Business Media.
02. Karr, A. F., 1981. Lanchester Attrition Processes and Theater-Level Combat Models. 1st ed. Virginia: Institute for Defense Analyses.
03. Newark, T., 2016. The History of Warfare. 1st ed. New York: Chartwell Books.
04. Ogiwara, T. & Usami, H., 2018. On the behavior of solutions for Lanchester square-law models with time-dependent coefficients. Josai Mathematical Monographs, Volume 11, p. 15–25.