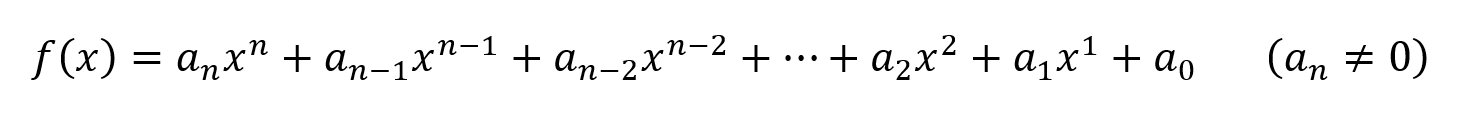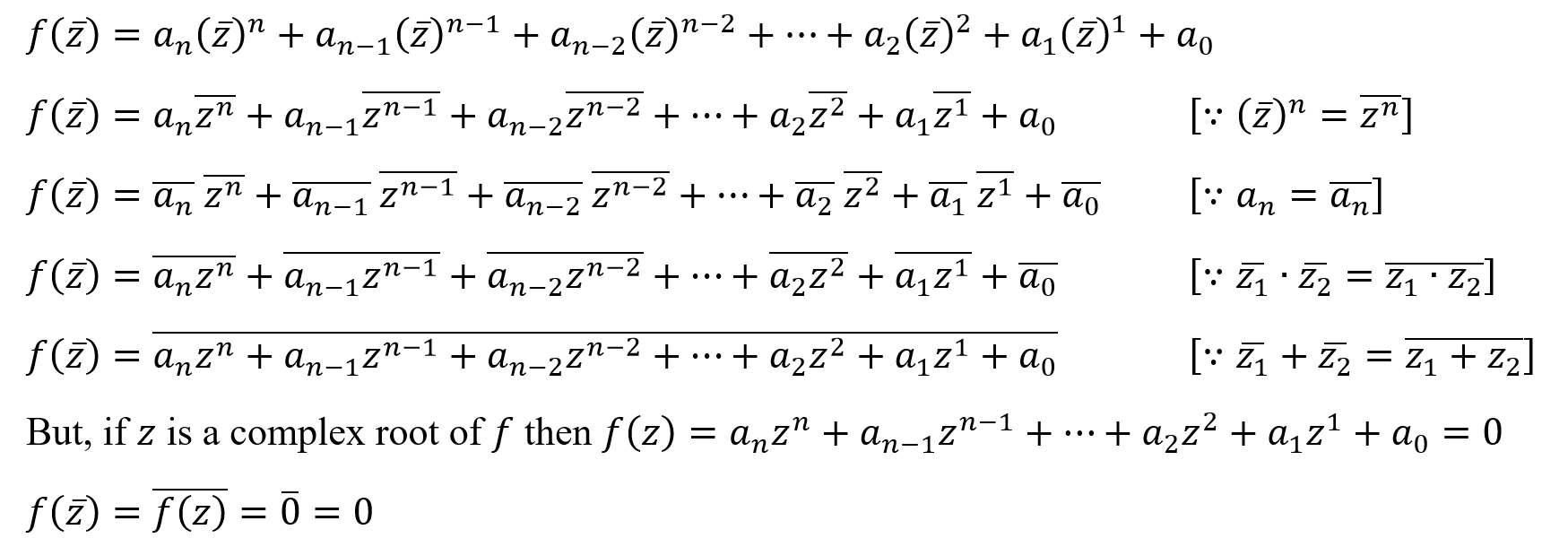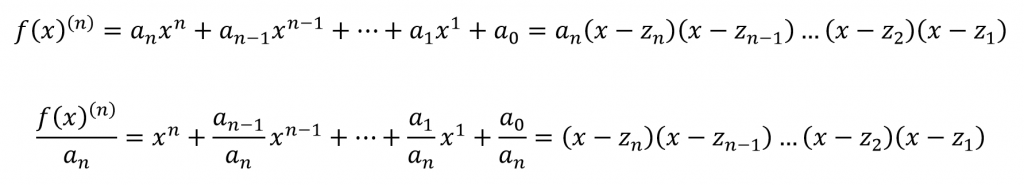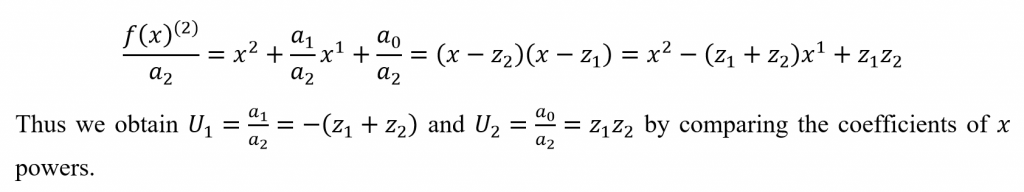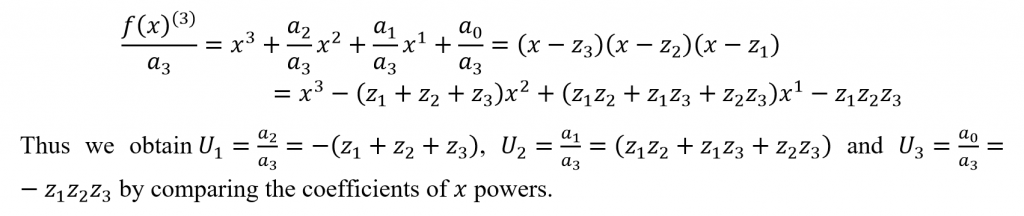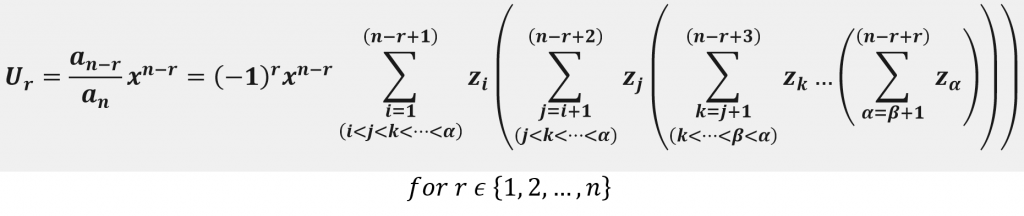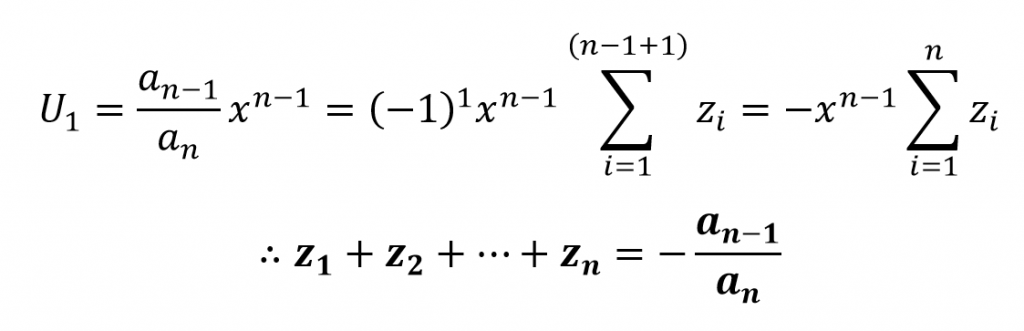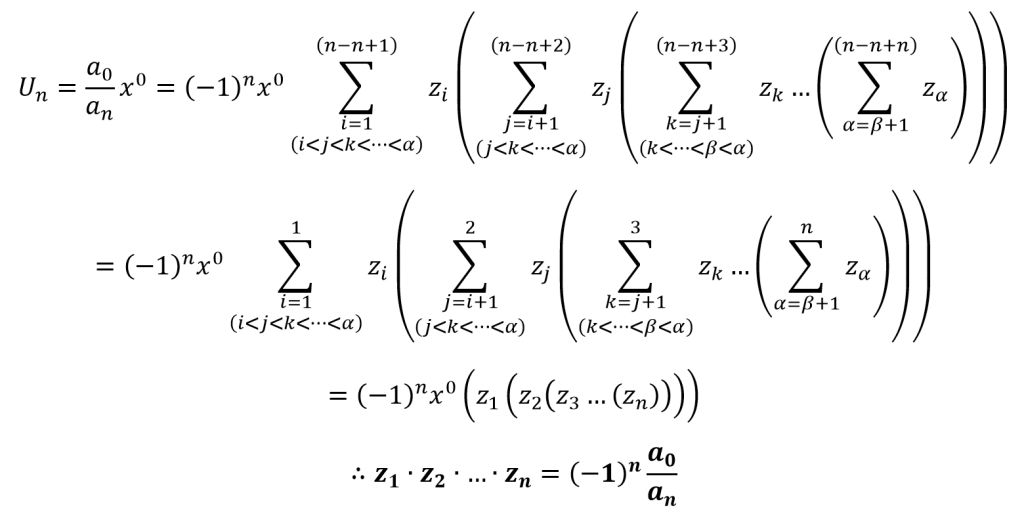Algebra, a topic in mathematics that crisscrosses from numbers that we can count and see to ideas that give rise to the foundations of mathematics itself, is a vast discussion. In the course of Abstract algebra, the exploration of rings, groups, and fields is prominent. However, to understand Abstract algebra, it’s easier to start with complex polynomials and work our way through.

For this, we shall start by taking a look at the general form of a polynomial function of degree n.

Here we can see that the domain and range of the function depends on which field the coefficients belong to. Let’s take that they belong to the field of complex numbers.

Fundamental Theorem of Algebra

Suppose that f is a univariate polynomial function of degree n with complex coefficients. Then f has at least one complex root.

In simple terms, this theorem guarantees the presence of a complex root in any polynomial with complex coefficients. We can also use this theorem to build up factors of complex polynomials. Let {z_i | for all i; f(z_i) = 0} be the set of all complex roots of the polynomial f(x).

From the Remainder theorem, we can express a function f(x) of degree n using a quotient Q(x) and remainder R(x) when divided by (x – k) as f(x)⁽ⁿ⁾ = Q(x)^(n-1)(x – k) + R(x). This can be extended to the Factor theorem which says that a root of a function is such that when divided by (x – k) the remainder is 0. Combining this and the Fundamental theorem of algebra we obtain the following.

It can be seen that the term Q_n(x)⁽⁰⁾, which is a constant coefficient, is the same as the leading coefficient of the polynomial function, a_n.

Conjugate Pairs Theorem

Suppose that f is a univariate polynomial function of degree n with real coefficients. Then if z is a root of f, the complex conjugate of z is also a root of f.

Let’s consider a polynomial of degree n as in above assume that z is a complex root of it. We can prove the above theorem as follows.

Thus we can see that the complex conjugate of a complex root of a polynomial function with real coefficients, is also a root of that function. From this, we can get a hint of a pairwise relationship between the complex roots of a polynomial.

Let’s revisit the factorization of f(x) outlined above again while applying the Conjugate pairs theorem to it.

But, for a fact, we know that i is always a natural number. From this, we can proceed to formulate the next theorem.

Real Factorization Theorem

Suppose that f is a univariate polynomial function of degree n with real coefficients. Then can be factorized into a product of linear factors corresponding to the real roots and an irreducible quadratic factor which will give the non-real roots of f.  

Combining this theorem with its predecessor gives us an important result. That is, if n is an odd number then there will exist at least one real root to the polynomial.

General Expansion of a Polynomial Function

From the Fundamental Theorem of Algebra, we saw that a polynomial function with complex coefficients can be factorized completely as follows.

Let’s consider n = 2 first.

Now consider n = 3.

From this, we can perceive the notion of a pattern occurring in the terms. This implies that a general term can be obtained. We can write this general term as follows.

To verify this, let’s compare the results for a 5th-degree polynomial.

Let’s consider the expansion for the power x^n-1 now.

Let’s consider the expansion for the power x⁰ now.

Inferences

Firstly, we have the idea that a polynomial function with complex coefficients can be reduced to factors of the complex roots. Secondly, we have the conclusion that if a complex root is present, its conjugate must follow as a root. Next, the ability to arrange a polynomial as a product of linear factors in the real plane and irreducible quadratic functions giving factors in the complex plane is established. Finally, we have the expansions of the powers x^{n – 1} and x⁰ in terms of the coefficients of the polynomial.

Utilizing all of these, we can now proceed to solve, say for example, z²⁴ – 1 = 0. This is in fact, the foundation for obtaining the n^th roots of unity.

References:

01. Kennedy, J. (n.d.). Some Polynomial Theorems. [Online] Available at https://monks.scranton.edu/files/courses/ProblemSolving/POLYTHEOREMS.pdf

02. Lankham, I., Nachtergaele, B., & Schilling, A. (n.d.). The Fundamental Theorem of Algebra. [Online] Available at https://www.math.ucdavis.edu/~anne/WQ2007/mat67-Ld-FTA.pdf

03. The Fundamental Theorem of Algebra. (n.d.). [Online] Available at http://155.101.98.133/~bertram/courses/4030/Fund.pdf

Featured Image Courtesy: https://bit.ly/3gY6lYV